Annulus Calculator
Entering the radii of the large and small circles to quickly calculate the circumference, area, and width of the annular shape.
Calculate the Circumference, Area, and Width of an Annulus
Circumference
Area
Width
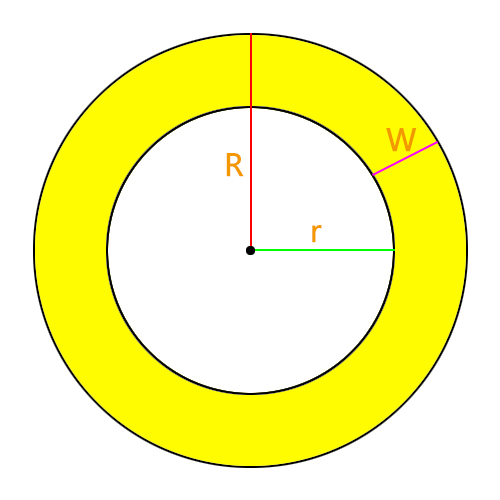
What is an Annulus?
An annulus is a geometric shape made up of two circles: the outer circle is the large circle, and the inner circle is the small circle. The shape of the annulus can be seen as the area remaining when a smaller circle is removed from a larger circle. The geometric properties of an annulus, such as its circumference, area, and width, are closely related to the radii of the large and small circles.
How to Calculate the Circumference, Area, and Width of an Annulus?
Circumference
The circumference of an annulus is the sum of the circumferences of the large and small circles. The formula is: \( P = 2\pi R + 2\pi r \)
Area
The area of the annulus is the area of the large circle minus the area of the small circle. The formula is: \( A = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) \)
Width
The width of the annulus is the difference between the radius of the large circle and the radius of the small circle. The formula is: \( W = R - r \) where R is the radius of the large circle and r is the radius of the small circle.
Examples
Example 1: Given the radius of the large circle as 8 and the radius of the small circle as 5, calculate the circumference, area, and width of the annulus.
Solution:
Circumference:
\( P = 2\pi (8) + 2\pi (5) = 2\pi(8 + 5) \approx 81.68 \)
Area:
\( A = \pi (8^2 - 5^2) = \pi (64 - 25) \approx 122.52 \)
Width:
\( W = 8 - 5 = 3 \)
Result: The circumference is approximately 81.68, the area is approximately 122.52, and the width is 3.
Example 2: Given the radius of the large circle as 12 and the radius of the small circle as 7, calculate the circumference, area, and width of the annulus.
Solution:
Circumference:
\( P = 2\pi (12) + 2\pi (7) = 2\pi(12 + 7) \approx 119.38 \)
Area:
\( A = \pi (12^2 - 7^2) = \pi (144 - 49) \approx 298.45 \)
Width:
\( W = 12 - 7 = 5 \)
Result: The circumference is approximately 119.38, the area is approximately 298.45, and the width is 5.