Arc Angle Calculator

What Is a Central Angle?

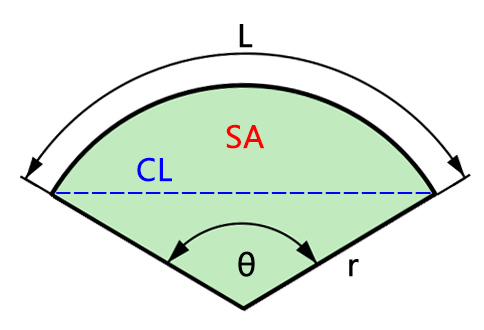
A central angle is the angle formed at the center of a circle, describing the size of the sector. With a known radius \( r \) and either arc length, chord length, or area, the central angle \( \theta \) can be calculated.

How to Calculate the Central Angle

1. Given Arc Length \( L \):

For Degrees: \( \theta = \frac{360 \times L}{2 \pi r} \) For Radians: \( \theta = \frac{L}{r} \)

2. Given Chord Length \( c \):

Rearrange the chord length formula: \( \theta = 2 \times \arcsin\left(\frac{c}{2r}\right) \) To convert radians to degrees: \( \theta_{\text{degrees}} = \theta_{\text{radians}} \times \frac{180}{\pi} \)

3. Given Area \( A \):

For Degrees: \( \theta = \frac{360 \times A}{\pi r^2} \) For Radians: \( \theta = \frac{2A}{r^2} \)

Examples

Example 1: Given the Radius \( r = 8 \) and Arc length \( L = 12 \), find the Central angle \( \theta \).

Example 2: Given the Radius \( r = 10 \) and Sector area \( A = 40 \), find the Central angle \( \theta \).