Arc Radius Calculator

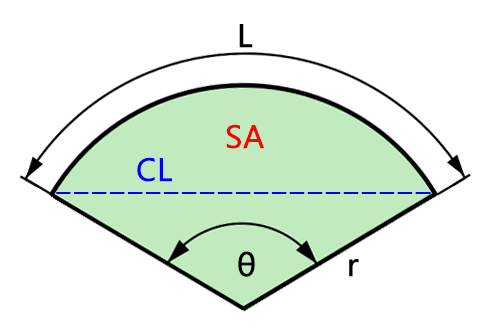
What Is a Sector Radius?

The radius of a sector is the distance from the center of the circle to the edge of the sector. With the central angle \( \theta \) and one known parameter (arc length, chord length, or area), you can calculate the radius \( r \).

How to Calculate the Radius of a Sector

1. Given Arc Length \( L \):

If \( \theta \) is in degrees: \( r = \frac{L \times 360}{2 \pi \theta} \) If \( \theta \) is in radians: \( r = \frac{L}{\theta} \)

2. Given Chord Length \( c \):

Rearrange the chord length formula to solve for \( r \): \( r = \frac{c}{2 \sin\left(\frac{\theta}{2}\right)} \) If \( \theta \) is in degrees, convert it to radians: \( \theta_{\text{radians}} = \theta_{\text{degrees}} \times \frac{\pi}{180} \)

3. Given Area \( A \):

If \( \theta \) is in degrees: \( r = \sqrt{\frac{A \times 360}{\pi \theta}} \) If \( \theta \) is in radians: \( r = \sqrt{\frac{2A}{\theta}} \)

Examples

Example 1: Given the Central angle \( \theta = 90^\circ \) and Arc length \( L = 15 \), Find the Sector radius \( r \)

Example 2: Given the Central angle \( \theta = 1.2 \) radians and Area \( A = 20 \), Find the Sector radius \( r \)