Arccotangent Calculator
Input a cotangent value to calculate its corresponding angle in degrees and radians.
Calculate arccot(x)
Degrees
Radians
What is the Arccotangent Function?
The arccotangent function, also called the inverse cotangent function, is the reverse of the cotangent function. It is typically denoted as \(\operatorname{arccot}(x)\) or \(\cot^{-1}(x)\). This function is used to calculate the angle that corresponds to a specific cotangent value. For the cotangent function \(y = \cot(\theta)\), the arccotangent is defined as: \( \theta = \operatorname{arccot}(x) \) Here: \(-\infty < x < \infty\), \(0 < \theta < \pi\). The range of the arccotangent function is \((0, \pi)\), ensuring that the function is unique and invertible.
Examples
Example 1: Find the angle for \(\cot(\theta) = 1\)
Solution:
\( \theta = \operatorname{arccot}(1) = \frac{\pi}{4} \approx 0.7854 \, \text{radians} \)
The angle corresponding to a cotangent value of 1 is \(\frac{\pi}{4}\) or 45°.
Example 2: Find the angle for \(\cot(\theta) = -1\)
Solution:
\( \theta = \operatorname{arccot}(-1) = \frac{3\pi}{4} \approx 2.3562 \, \text{radians} \)
The angle corresponding to a cotangent value of -1 is \(\frac{3\pi}{4}\) or 135°.
Graph of the Arccotangent Function
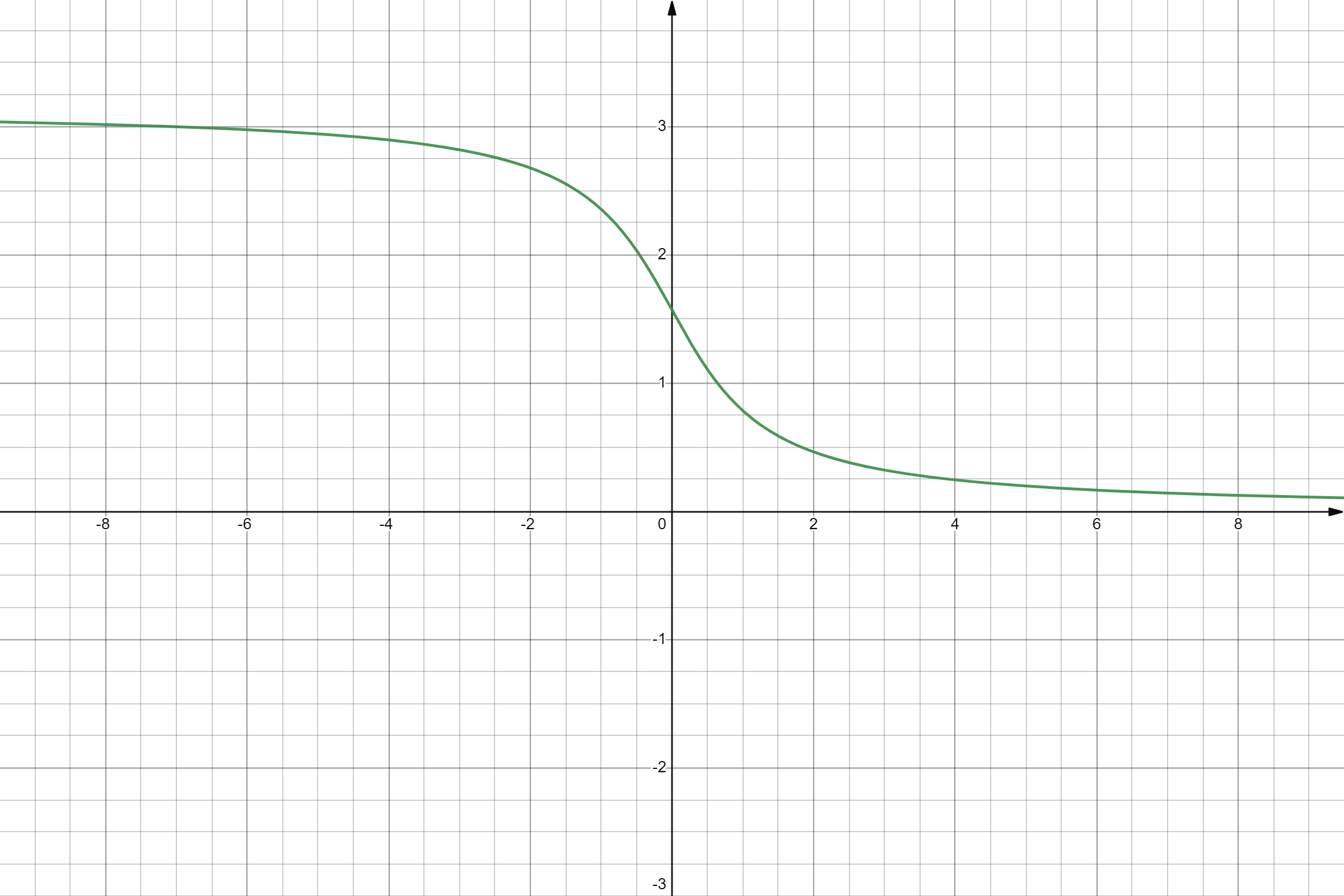
The graph of the arccotangent function is a smooth, monotonically decreasing curve that spans from \(-\infty\) to \(+\infty\). Key characteristics of the graph include:
- Domain: \((- \infty, +\infty)\)
- Range: \((0, \pi)\)
- Monotonicity: The arccotangent function is strictly decreasing over its domain.
- Symmetry: The function satisfies the property \(\operatorname{arccot}(-x) = \pi - \operatorname{arccot}(x)\), making it symmetric about \(\pi/2\).
Arccotangent Conversion Table
| Cotangent Value | Degrees | Radians |
|---|---|---|
| 57.28996163 | 1° | \(\frac{\pi}{180}\) |
| 28.63625328 | 2° | \(\frac{\pi}{90}\) |
| 19.08113669 | 3° | \(\frac{\pi}{60}\) |
| 14.30066626 | 4° | \(\frac{\pi}{45}\) |
| 11.4300523 | 5° | \(\frac{\pi}{36}\) |
| 9.51436445 | 6° | \(\frac{\pi}{30}\) |
| 8.14434643 | 7° | \(\frac{7\pi}{180}\) |
| 7.11536972 | 8° | \(\frac{2\pi}{45}\) |
| 6.31375151 | 9° | \(\frac{\pi}{20}\) |
| 5.67128182 | 10° | \(\frac{\pi}{18}\) |
| 5.14455402 | 11° | \(\frac{11\pi}{180}\) |
| 4.70463011 | 12° | \(\frac{\pi}{15}\) |
| 4.33147587 | 13° | \(\frac{13\pi}{180}\) |
| 4.01078093 | 14° | \(\frac{7\pi}{90}\) |
| 3.73205081 | 15° | \(\frac{\pi}{12}\) |
| 3.48741444 | 16° | \(\frac{4\pi}{45}\) |
| 3.27085262 | 17° | \(\frac{17\pi}{180}\) |
| 3.07768354 | 18° | \(\frac{\pi}{10}\) |
| 2.90421088 | 19° | \(\frac{19\pi}{180}\) |
| 2.74747742 | 20° | \(\frac{\pi}{9}\) |
| 2.60508906 | 21° | \(\frac{7\pi}{60}\) |
| 2.47508685 | 22° | \(\frac{11\pi}{90}\) |
| 2.35585237 | 23° | \(\frac{23\pi}{180}\) |
| 2.24603677 | 24° | \(\frac{2\pi}{15}\) |
| 2.14450692 | 25° | \(\frac{5\pi}{36}\) |
| 2.05030384 | 26° | \(\frac{13\pi}{90}\) |
| 1.96261051 | 27° | \(\frac{3\pi}{20}\) |
| 1.88072647 | 28° | \(\frac{7\pi}{45}\) |
| 1.80404776 | 29° | \(\frac{29\pi}{180}\) |
| 1.73205081 | 30° | \(\frac{\pi}{6}\) |
| 1.66427948 | 31° | \(\frac{31\pi}{180}\) |
| 1.60033453 | 32° | \(\frac{8\pi}{45}\) |
| 1.53986496 | 33° | \(\frac{11\pi}{60}\) |
| 1.48256097 | 34° | \(\frac{17\pi}{90}\) |
| 1.42814801 | 35° | \(\frac{7\pi}{36}\) |
| 1.37638192 | 36° | \(\frac{\pi}{5}\) |
| 1.32704482 | 37° | \(\frac{37\pi}{180}\) |
| 1.27994163 | 38° | \(\frac{19\pi}{90}\) |
| 1.23489716 | 39° | \(\frac{13\pi}{60}\) |
| 1.19175359 | 40° | \(\frac{2\pi}{9}\) |
| 1.15036841 | 41° | \(\frac{41\pi}{180}\) |
| 1.11061251 | 42° | \(\frac{7\pi}{30}\) |
| 1.07236871 | 43° | \(\frac{43\pi}{180}\) |
| 1.03553031 | 44° | \(\frac{11\pi}{45}\) |
| 1 | 45° | \(\frac{\pi}{4}\) |
| 0.96568877 | 46° | \(\frac{23\pi}{90}\) |
| 0.93251509 | 47° | \(\frac{47\pi}{180}\) |
| 0.90040404 | 48° | \(\frac{4\pi}{15}\) |
| 0.86928674 | 49° | \(\frac{49\pi}{180}\) |
| 0.83909963 | 50° | \(\frac{5\pi}{18}\) |
| 0.80978403 | 51° | \(\frac{17\pi}{60}\) |
| 0.78128563 | 52° | \(\frac{13\pi}{45}\) |
| 0.75355405 | 53° | \(\frac{53\pi}{180}\) |
| 0.72654253 | 54° | \(\frac{3\pi}{10}\) |
| 0.70020754 | 55° | \(\frac{11\pi}{36}\) |
| 0.67450852 | 56° | \(\frac{14\pi}{45}\) |
| 0.64940759 | 57° | \(\frac{19\pi}{60}\) |
| 0.62486935 | 58° | \(\frac{29\pi}{90}\) |
| 0.60086062 | 59° | \(\frac{59\pi}{180}\) |
| 0.57735027 | 60° | \(\frac{\pi}{3}\) |
| 0.55430905 | 61° | \(\frac{61\pi}{180}\) |
| 0.53170943 | 62° | \(\frac{31\pi}{90}\) |
| 0.50952545 | 63° | \(\frac{7\pi}{20}\) |
| 0.48773259 | 64° | \(\frac{16\pi}{45}\) |
| 0.46630766 | 65° | \(\frac{13\pi}{36}\) |
| 0.44522869 | 66° | \(\frac{11\pi}{30}\) |
| 0.42447482 | 67° | \(\frac{67\pi}{180}\) |
| 0.40402623 | 68° | \(\frac{17\pi}{45}\) |
| 0.38386404 | 69° | \(\frac{23\pi}{60}\) |
| 0.36397023 | 70° | \(\frac{7\pi}{18}\) |
| 0.34432761 | 71° | \(\frac{71\pi}{180}\) |
| 0.3249197 | 72° | \(\frac{2\pi}{5}\) |
| 0.30573068 | 73° | \(\frac{73\pi}{180}\) |
| 0.28674539 | 74° | \(\frac{37\pi}{90}\) |
| 0.26794919 | 75° | \(\frac{5\pi}{12}\) |
| 0.249328 | 76° | \(\frac{19\pi}{45}\) |
| 0.23086819 | 77° | \(\frac{77\pi}{180}\) |
| 0.21255656 | 78° | \(\frac{13\pi}{30}\) |
| 0.19438031 | 79° | \(\frac{79\pi}{180}\) |
| 0.17632698 | 80° | \(\frac{4\pi}{9}\) |
| 0.15838444 | 81° | \(\frac{9\pi}{20}\) |
| 0.14054083 | 82° | \(\frac{41\pi}{90}\) |
| 0.12278456 | 83° | \(\frac{83\pi}{180}\) |
| 0.10510424 | 84° | \(\frac{7\pi}{15}\) |
| 0.08748866 | 85° | \(\frac{17\pi}{36}\) |
| 0.06992681 | 86° | \(\frac{43\pi}{90}\) |
| 0.05240778 | 87° | \(\frac{29\pi}{60}\) |
| 0.03492077 | 88° | \(\frac{22\pi}{45}\) |
| 0.01745506 | 89° | \(\frac{89\pi}{180}\) |
| 0 | 90° | \(\frac{\pi}{2}\) |
| -0.01745506 | 91° | \(\frac{91\pi}{180}\) |
| -0.03492077 | 92° | \(\frac{23\pi}{45}\) |
| -0.05240778 | 93° | \(\frac{31\pi}{60}\) |
| -0.06992681 | 94° | \(\frac{47\pi}{90}\) |
| -0.08748866 | 95° | \(\frac{19\pi}{36}\) |
| -0.10510424 | 96° | \(\frac{8\pi}{15}\) |
| -0.12278456 | 97° | \(\frac{97\pi}{180}\) |
| -0.14054083 | 98° | \(\frac{49\pi}{90}\) |
| -0.15838444 | 99° | \(\frac{11\pi}{20}\) |
| -0.17632698 | 100° | \(\frac{5\pi}{9}\) |
| -0.19438031 | 101° | \(\frac{101\pi}{180}\) |
| -0.21255656 | 102° | \(\frac{17\pi}{30}\) |
| -0.23086819 | 103° | \(\frac{103\pi}{180}\) |
| -0.249328 | 104° | \(\frac{26\pi}{45}\) |
| -0.26794919 | 105° | \(\frac{7\pi}{12}\) |
| -0.28674539 | 106° | \(\frac{53\pi}{90}\) |
| -0.30573068 | 107° | \(\frac{107\pi}{180}\) |
| -0.3249197 | 108° | \(\frac{3\pi}{5}\) |
| -0.34432761 | 109° | \(\frac{109\pi}{180}\) |
| -0.36397023 | 110° | \(\frac{11\pi}{18}\) |
| -0.38386404 | 111° | \(\frac{37\pi}{60}\) |
| -0.40402623 | 112° | \(\frac{28\pi}{45}\) |
| -0.42447482 | 113° | \(\frac{113\pi}{180}\) |
| -0.44522869 | 114° | \(\frac{19\pi}{30}\) |
| -0.46630766 | 115° | \(\frac{23\pi}{36}\) |
| -0.48773259 | 116° | \(\frac{29\pi}{45}\) |
| -0.50952545 | 117° | \(\frac{13\pi}{20}\) |
| -0.53170943 | 118° | \(\frac{59\pi}{90}\) |
| -0.55430905 | 119° | \(\frac{119\pi}{180}\) |
| -0.57735027 | 120° | \(\frac{2\pi}{3}\) |
| -0.60086062 | 121° | \(\frac{121\pi}{180}\) |
| -0.62486935 | 122° | \(\frac{61\pi}{90}\) |
| -0.64940759 | 123° | \(\frac{41\pi}{60}\) |
| -0.67450852 | 124° | \(\frac{31\pi}{45}\) |
| -0.70020754 | 125° | \(\frac{25\pi}{36}\) |
| -0.72654253 | 126° | \(\frac{7\pi}{10}\) |
| -0.75355405 | 127° | \(\frac{127\pi}{180}\) |
| -0.78128563 | 128° | \(\frac{32\pi}{45}\) |
| -0.80978403 | 129° | \(\frac{43\pi}{60}\) |
| -0.83909963 | 130° | \(\frac{13\pi}{18}\) |
| -0.86928674 | 131° | \(\frac{131\pi}{180}\) |
| -0.90040404 | 132° | \(\frac{11\pi}{15}\) |
| -0.93251509 | 133° | \(\frac{133\pi}{180}\) |
| -0.96568877 | 134° | \(\frac{67\pi}{90}\) |
| -1 | 135° | \(\frac{3\pi}{4}\) |
| -1.03553031 | 136° | \(\frac{34\pi}{45}\) |
| -1.07236871 | 137° | \(\frac{137\pi}{180}\) |
| -1.11061251 | 138° | \(\frac{23\pi}{30}\) |
| -1.15036841 | 139° | \(\frac{139\pi}{180}\) |
| -1.19175359 | 140° | \(\frac{7\pi}{9}\) |
| -1.23489716 | 141° | \(\frac{47\pi}{60}\) |
| -1.27994163 | 142° | \(\frac{71\pi}{90}\) |
| -1.32704482 | 143° | \(\frac{143\pi}{180}\) |
| -1.37638192 | 144° | \(\frac{4\pi}{5}\) |
| -1.42814801 | 145° | \(\frac{29\pi}{36}\) |
| -1.48256097 | 146° | \(\frac{73\pi}{90}\) |
| -1.53986496 | 147° | \(\frac{49\pi}{60}\) |
| -1.60033453 | 148° | \(\frac{37\pi}{45}\) |
| -1.66427948 | 149° | \(\frac{149\pi}{180}\) |
| -1.73205081 | 150° | \(\frac{5\pi}{6}\) |
| -1.80404776 | 151° | \(\frac{151\pi}{180}\) |
| -1.88072647 | 152° | \(\frac{38\pi}{45}\) |
| -1.96261051 | 153° | \(\frac{17\pi}{20}\) |
| -2.05030384 | 154° | \(\frac{77\pi}{90}\) |
| -2.14450692 | 155° | \(\frac{31\pi}{36}\) |
| -2.24603677 | 156° | \(\frac{13\pi}{15}\) |
| -2.35585237 | 157° | \(\frac{157\pi}{180}\) |
| -2.47508685 | 158° | \(\frac{79\pi}{90}\) |
| -2.60508906 | 159° | \(\frac{53\pi}{60}\) |
| -2.74747742 | 160° | \(\frac{8\pi}{9}\) |
| -2.90421088 | 161° | \(\frac{161\pi}{180}\) |
| -3.07768354 | 162° | \(\frac{9\pi}{10}\) |
| -3.27085262 | 163° | \(\frac{163\pi}{180}\) |
| -3.48741444 | 164° | \(\frac{41\pi}{45}\) |
| -3.73205081 | 165° | \(\frac{11\pi}{12}\) |
| -4.01078093 | 166° | \(\frac{83\pi}{90}\) |
| -4.33147587 | 167° | \(\frac{167\pi}{180}\) |
| -4.70463011 | 168° | \(\frac{14\pi}{15}\) |
| -5.14455402 | 169° | \(\frac{169\pi}{180}\) |
| -5.67128182 | 170° | \(\frac{17\pi}{18}\) |
| -6.31375151 | 171° | \(\frac{19\pi}{20}\) |
| -7.11536972 | 172° | \(\frac{43\pi}{45}\) |
| -8.14434643 | 173° | \(\frac{173\pi}{180}\) |
| -9.51436445 | 174° | \(\frac{29\pi}{30}\) |
| -11.4300523 | 175° | \(\frac{35\pi}{36}\) |
| -14.30066626 | 176° | \(\frac{44\pi}{45}\) |
| -19.08113669 | 177° | \(\frac{59\pi}{60}\) |
| -28.63625328 | 178° | \(\frac{89\pi}{90}\) |
| -57.28996163 | 179° | \(\frac{179\pi}{180}\) |