Arccosecant Calculator
Input a cosecant value to compute the corresponding angle in degrees and radians.
Calculate arccsc(x)
Degrees
Radians
What is the Arccosecant Function?
The arccosecant function, also known as the inverse cosecant function, is the reverse of the cosecant function. It is typically represented by \(\operatorname{arccsc}(x)\) or \(\csc^{-1}(x)\). This function calculates the angle that corresponds to a given cosecant value. For the cosecant function \(y = \csc(\theta)\), the arccosecant function is defined as: \( \theta = \operatorname{arccsc}(x) \) Where: \(x \leq -1\) or \(x \geq 1\) (cosecant values outside of \(-1, 1\)), \(\theta\) lies within the range \([- \frac{\pi}{2}, \frac{\pi}{2}]\), excluding \(0\). This definition ensures that the arccosecant function is unique and invertible.
Examples
Example 1: Find the angle for \(\csc(\theta) = 2\)
Solution:
\( \theta = \operatorname{arccsc}(2) \approx 0.523 \, \text{radians} \)
The angle corresponding to a cosecant value of 2 is approximately 0.523 radians or 30°.
Example 2: Find the angle for \(\csc(\theta) = -2\)
Solution:
\( \theta = \operatorname{arccsc}(-2) \approx -0.523 \, \text{radians} \)
The angle corresponding to a cosecant value of -2 is approximately -0.523 radians or -30°.
Graph of the Arccosecant Function
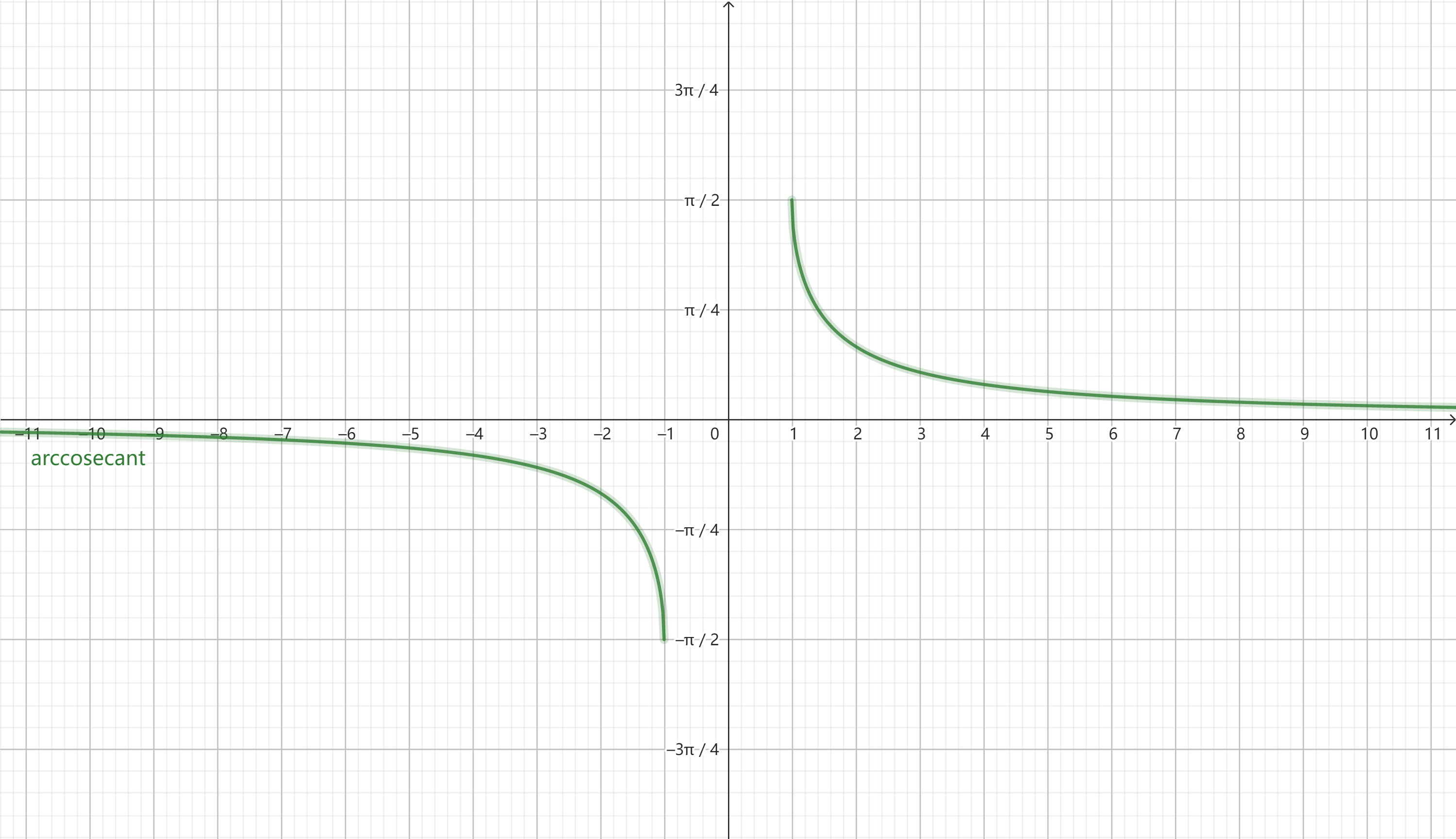
The graph of the arccosecant function consists of two curve segments: \((-\infty, -1] \cup [1, +\infty)\). Key Characteristics:
- Domain: \((-\infty, -1] \cup [1, +\infty)\)
- Range: \([- \frac{\pi}{2}, \frac{\pi}{2}]\), excluding \(0\).
- Monotonicity: The function is strictly decreasing in its domain.
- Symmetry: The arccosecant function satisfies the property \(\operatorname{arccsc}(-x) = -\operatorname{arccsc}(x)\), making it symmetric about the origin.
Arccosecant Conversion Table
| Cosecant Value | Degrees | Radians |
|---|---|---|
| -1 | -90° | \(\frac{-\pi}{2}\) |
| -1.00015233 | -89° | \(\frac{-89\pi}{180}\) |
| -1.00060954 | -88° | \(\frac{-22\pi}{45}\) |
| -1.00137235 | -87° | \(\frac{-29\pi}{60}\) |
| -1.0024419 | -86° | \(\frac{-43\pi}{90}\) |
| -1.00381984 | -85° | \(\frac{-17\pi}{36}\) |
| -1.00550828 | -84° | \(\frac{-7\pi}{15}\) |
| -1.00750983 | -83° | \(\frac{-83\pi}{180}\) |
| -1.00982757 | -82° | \(\frac{-41\pi}{90}\) |
| -1.01246513 | -81° | \(\frac{-9\pi}{20}\) |
| -1.01542661 | -80° | \(\frac{-4\pi}{9}\) |
| -1.01871669 | -79° | \(\frac{-79\pi}{180}\) |
| -1.02234059 | -78° | \(\frac{-13\pi}{30}\) |
| -1.02630411 | -77° | \(\frac{-77\pi}{180}\) |
| -1.03061363 | -76° | \(\frac{-19\pi}{45}\) |
| -1.03527618 | -75° | \(\frac{-5\pi}{12}\) |
| -1.04029944 | -74° | \(\frac{-37\pi}{90}\) |
| -1.04569176 | -73° | \(\frac{-73\pi}{180}\) |
| -1.05146222 | -72° | \(\frac{-2\pi}{5}\) |
| -1.05762068 | -71° | \(\frac{-71\pi}{180}\) |
| -1.06417777 | -70° | \(\frac{-7\pi}{18}\) |
| -1.07114499 | -69° | \(\frac{-23\pi}{60}\) |
| -1.07853474 | -68° | \(\frac{-17\pi}{45}\) |
| -1.08636038 | -67° | \(\frac{-67\pi}{180}\) |
| -1.09463628 | -66° | \(\frac{-11\pi}{30}\) |
| -1.10337792 | -65° | \(\frac{-13\pi}{36}\) |
| -1.11260194 | -64° | \(\frac{-16\pi}{45}\) |
| -1.12232624 | -63° | \(\frac{-7\pi}{20}\) |
| -1.13257005 | -62° | \(\frac{-31\pi}{90}\) |
| -1.14335407 | -61° | \(\frac{-61\pi}{180}\) |
| -1.15470054 | -60° | \(\frac{-\pi}{3}\) |
| -1.1666334 | -59° | \(\frac{-59\pi}{180}\) |
| -1.1791784 | -58° | \(\frac{-29\pi}{90}\) |
| -1.19236329 | -57° | \(\frac{-19\pi}{60}\) |
| -1.20621795 | -56° | \(\frac{-14\pi}{45}\) |
| -1.22077459 | -55° | \(\frac{-11\pi}{36}\) |
| -1.23606798 | -54° | \(\frac{-3\pi}{10}\) |
| -1.25213566 | -53° | \(\frac{-53\pi}{180}\) |
| -1.26901822 | -52° | \(\frac{-13\pi}{45}\) |
| -1.28675957 | -51° | \(\frac{-17\pi}{60}\) |
| -1.30540729 | -50° | \(\frac{-5\pi}{18}\) |
| -1.32501299 | -49° | \(\frac{-49\pi}{180}\) |
| -1.34563273 | -48° | \(\frac{-4\pi}{15}\) |
| -1.36732746 | -47° | \(\frac{-47\pi}{180}\) |
| -1.39016359 | -46° | \(\frac{-23\pi}{90}\) |
| -1.41421356 | -45° | \(\frac{-\pi}{4}\) |
| -1.43955654 | -44° | \(\frac{-11\pi}{45}\) |
| -1.46627919 | -43° | \(\frac{-43\pi}{180}\) |
| -1.49447655 | -42° | \(\frac{-7\pi}{30}\) |
| -1.52425309 | -41° | \(\frac{-41\pi}{180}\) |
| -1.55572383 | -40° | \(\frac{-2\pi}{9}\) |
| -1.58901573 | -39° | \(\frac{-13\pi}{60}\) |
| -1.62426925 | -38° | \(\frac{-19\pi}{90}\) |
| -1.66164014 | -37° | \(\frac{-37\pi}{180}\) |
| -1.70130162 | -36° | \(\frac{-\pi}{5}\) |
| -1.7434468 | -35° | \(\frac{-7\pi}{36}\) |
| -1.78829165 | -34° | \(\frac{-17\pi}{90}\) |
| -1.83607846 | -33° | \(\frac{-11\pi}{60}\) |
| -1.88707991 | -32° | \(\frac{-8\pi}{45}\) |
| -1.94160403 | -31° | \(\frac{-31\pi}{180}\) |
| -2 | -30° | \(\frac{-\pi}{6}\) |
| -2.06266534 | -29° | \(\frac{-29\pi}{180}\) |
| -2.13005447 | -28° | \(\frac{-7\pi}{45}\) |
| -2.20268926 | -27° | \(\frac{-3\pi}{20}\) |
| -2.28117203 | -26° | \(\frac{-13\pi}{90}\) |
| -2.36620158 | -25° | \(\frac{-5\pi}{36}\) |
| -2.45859334 | -24° | \(\frac{-2\pi}{15}\) |
| -2.55930467 | -23° | \(\frac{-23\pi}{180}\) |
| -2.66946716 | -22° | \(\frac{-11\pi}{90}\) |
| -2.79042811 | -21° | \(\frac{-7\pi}{60}\) |
| -2.9238044 | -20° | \(\frac{-\pi}{9}\) |
| -3.07155349 | -19° | \(\frac{-19\pi}{180}\) |
| -3.23606798 | -18° | \(\frac{-\pi}{10}\) |
| -3.42030362 | -17° | \(\frac{-17\pi}{180}\) |
| -3.62795528 | -16° | \(\frac{-4\pi}{45}\) |
| -3.86370331 | -15° | \(\frac{-\pi}{12}\) |
| -4.13356549 | -14° | \(\frac{-7\pi}{90}\) |
| -4.44541148 | -13° | \(\frac{-13\pi}{180}\) |
| -4.80973434 | -12° | \(\frac{-\pi}{15}\) |
| -5.24084306 | -11° | \(\frac{-11\pi}{180}\) |
| -5.75877048 | -10° | \(\frac{-\pi}{18}\) |
| -6.39245322 | -9° | \(\frac{-\pi}{20}\) |
| -7.18529653 | -8° | \(\frac{-2\pi}{45}\) |
| -8.20550905 | -7° | \(\frac{-7\pi}{180}\) |
| -9.56677223 | -6° | \(\frac{-\pi}{30}\) |
| -11.47371325 | -5° | \(\frac{-\pi}{36}\) |
| -14.33558703 | -4° | \(\frac{-\pi}{45}\) |
| -19.10732261 | -3° | \(\frac{-\pi}{60}\) |
| -28.65370835 | -2° | \(\frac{-\pi}{90}\) |
| -57.2986885 | -1° | \(\frac{-\pi}{180}\) |
| 57.2986885 | 1° | \(\frac{\pi}{180}\) |
| 28.65370835 | 2° | \(\frac{\pi}{90}\) |
| 19.10732261 | 3° | \(\frac{\pi}{60}\) |
| 14.33558703 | 4° | \(\frac{\pi}{45}\) |
| 11.47371325 | 5° | \(\frac{\pi}{36}\) |
| 9.56677223 | 6° | \(\frac{\pi}{30}\) |
| 8.20550905 | 7° | \(\frac{7\pi}{180}\) |
| 7.18529653 | 8° | \(\frac{2\pi}{45}\) |
| 6.39245322 | 9° | \(\frac{\pi}{20}\) |
| 5.75877048 | 10° | \(\frac{\pi}{18}\) |
| 5.24084306 | 11° | \(\frac{11\pi}{180}\) |
| 4.80973434 | 12° | \(\frac{\pi}{15}\) |
| 4.44541148 | 13° | \(\frac{13\pi}{180}\) |
| 4.13356549 | 14° | \(\frac{7\pi}{90}\) |
| 3.86370331 | 15° | \(\frac{\pi}{12}\) |
| 3.62795528 | 16° | \(\frac{4\pi}{45}\) |
| 3.42030362 | 17° | \(\frac{17\pi}{180}\) |
| 3.23606798 | 18° | \(\frac{\pi}{10}\) |
| 3.07155349 | 19° | \(\frac{19\pi}{180}\) |
| 2.9238044 | 20° | \(\frac{\pi}{9}\) |
| 2.79042811 | 21° | \(\frac{7\pi}{60}\) |
| 2.66946716 | 22° | \(\frac{11\pi}{90}\) |
| 2.55930467 | 23° | \(\frac{23\pi}{180}\) |
| 2.45859334 | 24° | \(\frac{2\pi}{15}\) |
| 2.36620158 | 25° | \(\frac{5\pi}{36}\) |
| 2.28117203 | 26° | \(\frac{13\pi}{90}\) |
| 2.20268926 | 27° | \(\frac{3\pi}{20}\) |
| 2.13005447 | 28° | \(\frac{7\pi}{45}\) |
| 2.06266534 | 29° | \(\frac{29\pi}{180}\) |
| 2 | 30° | \(\frac{\pi}{6}\) |
| 1.94160403 | 31° | \(\frac{31\pi}{180}\) |
| 1.88707991 | 32° | \(\frac{8\pi}{45}\) |
| 1.83607846 | 33° | \(\frac{11\pi}{60}\) |
| 1.78829165 | 34° | \(\frac{17\pi}{90}\) |
| 1.7434468 | 35° | \(\frac{7\pi}{36}\) |
| 1.70130162 | 36° | \(\frac{\pi}{5}\) |
| 1.66164014 | 37° | \(\frac{37\pi}{180}\) |
| 1.62426925 | 38° | \(\frac{19\pi}{90}\) |
| 1.58901573 | 39° | \(\frac{13\pi}{60}\) |
| 1.55572383 | 40° | \(\frac{2\pi}{9}\) |
| 1.52425309 | 41° | \(\frac{41\pi}{180}\) |
| 1.49447655 | 42° | \(\frac{7\pi}{30}\) |
| 1.46627919 | 43° | \(\frac{43\pi}{180}\) |
| 1.43955654 | 44° | \(\frac{11\pi}{45}\) |
| 1.41421356 | 45° | \(\frac{\pi}{4}\) |
| 1.39016359 | 46° | \(\frac{23\pi}{90}\) |
| 1.36732746 | 47° | \(\frac{47\pi}{180}\) |
| 1.34563273 | 48° | \(\frac{4\pi}{15}\) |
| 1.32501299 | 49° | \(\frac{49\pi}{180}\) |
| 1.30540729 | 50° | \(\frac{5\pi}{18}\) |
| 1.28675957 | 51° | \(\frac{17\pi}{60}\) |
| 1.26901822 | 52° | \(\frac{13\pi}{45}\) |
| 1.25213566 | 53° | \(\frac{53\pi}{180}\) |
| 1.23606798 | 54° | \(\frac{3\pi}{10}\) |
| 1.22077459 | 55° | \(\frac{11\pi}{36}\) |
| 1.20621795 | 56° | \(\frac{14\pi}{45}\) |
| 1.19236329 | 57° | \(\frac{19\pi}{60}\) |
| 1.1791784 | 58° | \(\frac{29\pi}{90}\) |
| 1.1666334 | 59° | \(\frac{59\pi}{180}\) |
| 1.15470054 | 60° | \(\frac{\pi}{3}\) |
| 1.14335407 | 61° | \(\frac{61\pi}{180}\) |
| 1.13257005 | 62° | \(\frac{31\pi}{90}\) |
| 1.12232624 | 63° | \(\frac{7\pi}{20}\) |
| 1.11260194 | 64° | \(\frac{16\pi}{45}\) |
| 1.10337792 | 65° | \(\frac{13\pi}{36}\) |
| 1.09463628 | 66° | \(\frac{11\pi}{30}\) |
| 1.08636038 | 67° | \(\frac{67\pi}{180}\) |
| 1.07853474 | 68° | \(\frac{17\pi}{45}\) |
| 1.07114499 | 69° | \(\frac{23\pi}{60}\) |
| 1.06417777 | 70° | \(\frac{7\pi}{18}\) |
| 1.05762068 | 71° | \(\frac{71\pi}{180}\) |
| 1.05146222 | 72° | \(\frac{2\pi}{5}\) |
| 1.04569176 | 73° | \(\frac{73\pi}{180}\) |
| 1.04029944 | 74° | \(\frac{37\pi}{90}\) |
| 1.03527618 | 75° | \(\frac{5\pi}{12}\) |
| 1.03061363 | 76° | \(\frac{19\pi}{45}\) |
| 1.02630411 | 77° | \(\frac{77\pi}{180}\) |
| 1.02234059 | 78° | \(\frac{13\pi}{30}\) |
| 1.01871669 | 79° | \(\frac{79\pi}{180}\) |
| 1.01542661 | 80° | \(\frac{4\pi}{9}\) |
| 1.01246513 | 81° | \(\frac{9\pi}{20}\) |
| 1.00982757 | 82° | \(\frac{41\pi}{90}\) |
| 1.00750983 | 83° | \(\frac{83\pi}{180}\) |
| 1.00550828 | 84° | \(\frac{7\pi}{15}\) |
| 1.00381984 | 85° | \(\frac{17\pi}{36}\) |
| 1.0024419 | 86° | \(\frac{43\pi}{90}\) |
| 1.00137235 | 87° | \(\frac{29\pi}{60}\) |
| 1.00060954 | 88° | \(\frac{22\pi}{45}\) |
| 1.00015233 | 89° | \(\frac{89\pi}{180}\) |
| 1 | 90° | \(\frac{\pi}{2}\) |