Circular Segment Calculator
Entering the central angle and one known property value (such as radius, chord length, arc length, area, etc.) to quickly compute the radius, chord length, arc length, area, and other properties of a circular segment.
Calculate the Radius, Chord Length, Arc Length, Perimeter, Area, Height, and More
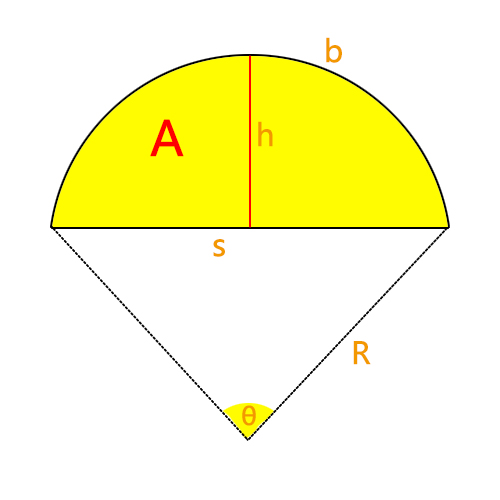
Radius
Chord Length
Arc Length
Height
Perimeter
Area
What is a Circular Segment?
A circular segment is the region enclosed by a circular arc and the chord corresponding to that arc. It is described by a central angle (in degrees or radians) and properties such as arc length, chord length, height, perimeter, and area.
How to Calculate the Properties of a Circular Segment?
Let θ be the central angle of the circular segment (in radians) and r be the radius of the circle.
Chord Length
The chord length is the straight-line distance between two points on the circle, calculated using the formula: \( \text{Chord Length} = 2 \times r \times \sin\left(\frac{\theta}{2}\right) \)
Arc Length
The arc length is the length of the circular arc, which can be calculated by: \( \text{Arc Length} = \theta \times r \)
Height
The height is the perpendicular distance from the top of the circular segment to the chord, calculated as: \( h = r - \sqrt{r^2 - \left(\frac{\text{Chord Length}}{2}\right)^2} \) where Chord Length is the chord length.
Perimeter
The perimeter of the circular segment is the sum of the arc length and the chord length: \( P = \text{Arc Length} + \text{Chord Length} \)
Area
The area of the circular segment is the area of the sector corresponding to the central angle minus the area of the triangle formed by the radius and chord: \( A = \frac{1}{2} r^2 (\theta - \sin\theta) \)
Example: Given the central angle θ = 60° and the radius r = 10, calculate the chord length, arc length, height, perimeter, and area of the circular segment.
Solution:
Convert the angle to radians:
\( \theta = 60^\circ = \frac{60 \times \pi}{180} = \frac{\pi}{3} \text{ rad} \)
Chord Length:
\( \text{Chord Length} = 2 \times 10 \times \sin\left(\frac{\pi}{6}\right) = 20 \times \frac{1}{2} = 10 \)
Arc Length:
\( \text{Arc Length} = \theta \times r = \frac{\pi}{3} \times 10 \approx 10.47 \)
Height:
\( h = 10 - \sqrt{10^2 - \left(\frac{10}{2}\right)^2} = 10 - \sqrt{100 - 25} \approx 1.34 \)
Perimeter:
\( P = \text{Arc Length} + \text{Chord Length} = 10.47 + 10 = 20.47 \)
Area:
\( A = \frac{1}{2} \times 10^2 \times \left(\frac{\pi}{3} - \sin\left(\frac{\pi}{3}\right)\right) \approx 9.06 \)