Cosecant Calculator

Enter any angle or radian to calculate the corresponding cosecant value.

Calculate csc(θ)

Result

What Is Cosecant?

The cosecant function ( $\csc (θ)$ ) is one of the six main trigonometric functions. It is typically expressed as the ratio of the hypotenuse to the opposite side in a right triangle.

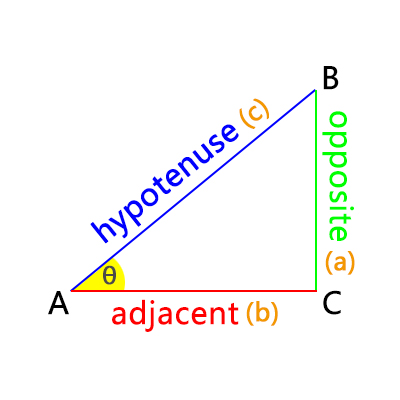
In a right triangle, the cosecant of an angle $θ$ is defined as: $\csc (θ) = \frac{Hypotenuse}{Opposite} = \frac{c}{a}$ This means that cosecant represents the ratio of the hypotenuse to the opposite side of an angle.

On the unit circle, the cosecant of an angle $θ$ is defined as: $\csc (θ) = \frac{1}{\sin (θ)}$ This shows that cosecant is the reciprocal of the sine function.

Examples

Example 1: Calculating Cosecant in a Right Triangle

Consider a right triangle where one angle is $θ = 30^{\circ}$ , the length of the opposite side is 5, and the hypotenuse is 10.

Solution:

Using the definition of cosecant:

$\csc (30^{\circ}) = \frac{10}{5} = 2$

Thus, the cosecant of $30^{\circ}$ is 2.

Example 2: Real-World Application

Suppose you are calculating the slope of a hill with an angle of $θ = 60^{\circ}$ . You need to determine its cosecant value.

Solution:

Using the definition of cosecant:

$\csc (60^{\circ}) = \frac{1}{\sin (60^{\circ})} = \frac{1}{0.866} \approx 1.155$

Thus, the cosecant of $60^{\circ}$ is approximately 1.155.

Graph and Properties of Cosecant

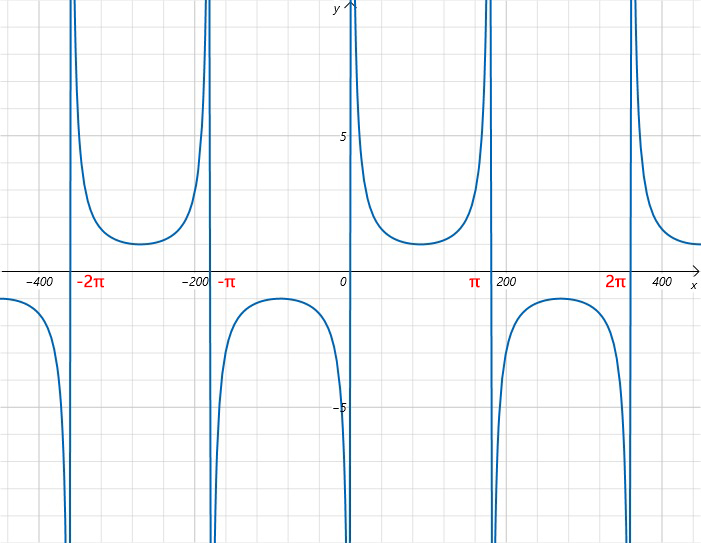
The graph of the cosecant function exhibits periodic behavior and features vertical asymptotes. Below are some key properties:

Periodicity: The cosecant function repeats every $2 π$ radians (or 360°).
Odd Function: Cosecant is an odd function, meaning $\csc (- θ) = - \csc (θ)$ . Its graph is symmetric about the origin.
Amplitude: The amplitude of the cosecant function is unlimited, with values ranging from negative infinity to positive infinity.
Asymptotes: Vertical asymptotes occur at $θ = n π$ (where $n$ is an integer), where the function approaches infinity or negative infinity.
Domain and Range
- Domain: All angles except $n π$ (where $n$ is an integer).
- Range: $(- \infty, - 1] \cup [1, \infty)$ .

Quadrant Behavior of Cosecant

The sign and behavior of cosecant in different quadrants are as follows:

Quadrant	Degrees	Radians	Sign	Range	Monotonicity
1st Quadrant	$0^{\circ}$ - $90^{\circ}$	$0$ - $\frac{π}{2}$	Positive	$(\infty, 1]$	Decreasing
2nd Quadrant	$90^{\circ}$ - $180^{\circ}$	$\frac{π}{2}$ - $π$	Positive	$[1, \infty)$	Increasing
3rd Quadrant	$180^{\circ}$ - $270^{\circ}$	$π$ - $\frac{3 π}{2}$	Negative	$(- \infty, - 1]$	Increasing
4th Quadrant	$270^{\circ}$ - $360^{\circ}$	$\frac{3 π}{2}$ - $2 π$	Negative	$[- 1, - \infty)$	Decreasing

Other Cosecant Calculations

1. Reciprocal of Cosecant (Sine Function)

The reciprocal of the cosecant function is the sine function ( $\sin (θ)$ ): $\frac{1}{\csc (θ)} = \sin (θ)$ Note: Sine is undefined when $\csc (θ) = 0$ .

2. Derivative of Cosecant

The derivative of the cosecant function is: $\frac{d}{d θ} \csc (θ) = - \csc (θ) \cot (θ)$

3. Integral of Cosecant

The integral of the cosecant function is: $\int \csc (θ) d θ = - \ln | \csc (θ) + \cot (θ) | + C$

4. Inverse Cosecant Function (arccsc)

The inverse cosecant function ( $arccsc (x)$ ) finds the angle $θ$ corresponding to a given cosecant value $x$ : $θ = arccsc (x)$

Cosecant Table of Common Values

Degree	Radian	Cosecant Value
5°	$\frac{π}{36}$	11.47371325
10°	$\frac{π}{18}$	5.75877048
15°	$\frac{π}{12}$	3.86370331
20°	$\frac{π}{9}$	2.9238044
25°	$\frac{5 π}{36}$	2.36620158
30°	$\frac{π}{6}$	2
35°	$\frac{7 π}{36}$	1.7434468
40°	$\frac{2 π}{9}$	1.55572383
45°	$\frac{π}{4}$	1.41421356
50°	$\frac{5 π}{18}$	1.30540729
55°	$\frac{11 π}{36}$	1.22077459
60°	$\frac{π}{3}$	1.15470054
65°	$\frac{13 π}{36}$	1.10337792
70°	$\frac{7 π}{18}$	1.06417777
75°	$\frac{5 π}{12}$	1.03527618
80°	$\frac{4 π}{9}$	1.01542661
85°	$\frac{17 π}{36}$	1.00381984
90°	$\frac{π}{2}$	1
95°	$\frac{19 π}{36}$	1.00381984
100°	$\frac{5 π}{9}$	1.01542661
105°	$\frac{7 π}{12}$	1.03527618
110°	$\frac{11 π}{18}$	1.06417777
115°	$\frac{23 π}{36}$	1.10337792
120°	$\frac{2 π}{3}$	1.15470054
125°	$\frac{25 π}{36}$	1.22077459
130°	$\frac{13 π}{18}$	1.30540729
135°	$\frac{3 π}{4}$	1.41421356
140°	$\frac{7 π}{9}$	1.55572383
145°	$\frac{29 π}{36}$	1.7434468
150°	$\frac{5 π}{6}$	2
155°	$\frac{31 π}{36}$	2.36620158
160°	$\frac{8 π}{9}$	2.9238044
165°	$\frac{11 π}{12}$	3.86370331
170°	$\frac{17 π}{18}$	5.75877048
175°	$\frac{35 π}{36}$	11.47371325
185°	$\frac{37 π}{36}$	-11.47371325
190°	$\frac{19 π}{18}$	-5.75877048
195°	$\frac{13 π}{12}$	-3.86370331
200°	$\frac{10 π}{9}$	-2.9238044
205°	$\frac{41 π}{36}$	-2.36620158
210°	$\frac{7 π}{6}$	-2
215°	$\frac{43 π}{36}$	-1.7434468
220°	$\frac{11 π}{9}$	-1.55572383
225°	$\frac{5 π}{4}$	-1.41421356
230°	$\frac{23 π}{18}$	-1.30540729
235°	$\frac{47 π}{36}$	-1.22077459
240°	$\frac{4 π}{3}$	-1.15470054
245°	$\frac{49 π}{36}$	-1.10337792
250°	$\frac{25 π}{18}$	-1.06417777
255°	$\frac{17 π}{12}$	-1.03527618
260°	$\frac{13 π}{9}$	-1.01542661
265°	$\frac{53 π}{36}$	-1.00381984
270°	$\frac{3 π}{2}$	-1
275°	$\frac{55 π}{36}$	-1.00381984
280°	$\frac{14 π}{9}$	-1.01542661
285°	$\frac{19 π}{12}$	-1.03527618
290°	$\frac{29 π}{18}$	-1.06417777
295°	$\frac{59 π}{36}$	-1.10337792
300°	$\frac{5 π}{3}$	-1.15470054
305°	$\frac{61 π}{36}$	-1.22077459
310°	$\frac{31 π}{18}$	-1.30540729
315°	$\frac{7 π}{4}$	-1.41421356
320°	$\frac{16 π}{9}$	-1.55572383
325°	$\frac{65 π}{36}$	-1.7434468
330°	$\frac{11 π}{6}$	-2
335°	$\frac{67 π}{36}$	-2.36620158
340°	$\frac{17 π}{9}$	-2.9238044
345°	$\frac{23 π}{12}$	-3.86370331
350°	$\frac{35 π}{18}$	-5.75877048
355°	$\frac{71 π}{36}$	-11.47371325