Ellipse Calculator

Entering the semi-major axis and semi-minor axis to quickly calculate the ellipse's circumference, area, and eccentricity.

Calculate the Ellipse's Circumference, Area, and Eccentricity

Circumference

Area

Eccentricity

What is an Ellipse?

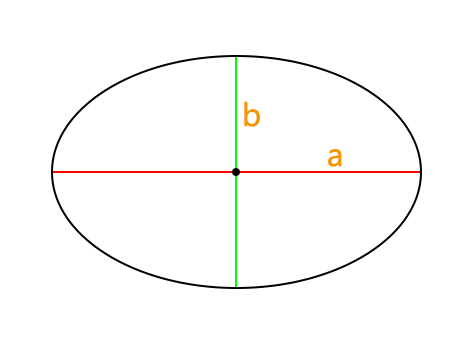
An ellipse is the set of points on a plane where the sum of the distances to two fixed points, called foci, remains constant. The two axes of an ellipse are the semi-major axis and the semi-minor axis. The semi-major axis is the radius along the longest direction of the ellipse, while the semi-minor axis is the radius along the shortest direction. The circumference, area, and eccentricity of an ellipse can be calculated using the known values of the semi-major and semi-minor axes.

How to Calculate the Circumference of an Ellipse?

Because the exact formula for calculating the circumference of an ellipse is quite complex, an approximate formula is typically used: \( P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \)

How to Calculate the Area of an Ellipse?

The formula for calculating the area of an ellipse is: \( A = \pi a b \)

How to Calculate the Eccentricity of an Ellipse?

The eccentricity e represents how "flattened" the ellipse is, and is calculated using the formula: \( e = \sqrt{1 - \frac{b^2}{a^2}} \) where a is the semi-major axis and b is the semi-minor axis.

Examples

Example 1: Given the semi-major axis of the ellipse as 6 and the semi-minor axis as 4, calculate the circumference, area, and eccentricity.

Solution:

Circumference:

\( P \approx \pi \left[ 3(6 + 4) - \sqrt{(3 \times 6 + 4)(6 + 3 \times 4)} \right] \approx 31.73 \)

Area:

\( A = \pi \times 6 \times 4 = 24\pi \approx 75.398 \)

Eccentricity:

\( e = \sqrt{1 - \frac{4^2}{6^2}} \approx 0.745 \)

Example 2: Given the semi-major axis of the ellipse as 10 and the semi-minor axis as 6, calculate the circumference, area, and eccentricity.