Golden Ratio Calculator
Input either a part length or the total length to calculate the remaining values according to the golden ratio.
Calculate the Missing Lengths in a Golden Ratio
Result
What Is the Golden Ratio?
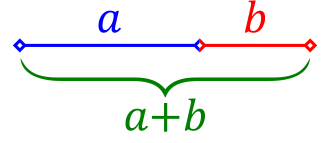
The golden ratio is a unique proportional relationship, often represented as: \( \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \) When a total length \( L \) is divided into two parts \( a \) (longer part) and \( b \) (shorter part), the golden ratio satisfies: \( \frac{L}{a} = \frac{a}{b} = \phi \)
How to Calculate the Missing Lengths in a Golden Ratio?
- If the longer part \( a \) is known: Calculate the shorter part: \( b = \frac{a}{\phi} \) Calculate the total length: \( L = a + b \)
- If the shorter part \( b \) is known: Calculate the longer part: \( a = b \times \phi \) Calculate the total length: \( L = a + b \)
- If the total length \( L \) is known: Calculate the longer part: \( a = \frac{L}{\phi + 1} \) Calculate the shorter part: \( b = L - a \)
Examples
Example 1: Given Longer part \( a = 100 \), Find Shorter part \( b \) and total length \( L \)
Solution:
1. Shorter part:
\( b = \frac{100}{1.618} \approx 61.8 \)
2. Total length:
\( L = a + b = 100 + 61.8 = 161.8 \)
Result: Shorter part \( b \approx 61.8 \), total length \( L \approx 161.8 \).
Example 2: Given Total length \( L = 200 \), Find Longer part \( a \) and shorter part \( b \)
Solution:
1. Longer part:
\( a = \frac{200}{1.618 + 1} \approx 123.6 \)
2. Shorter part:
\( b = L - a = 200 - 123.6 = 76.4 \)
Result: Longer part \( a \approx 123.6 \), shorter part \( b \approx 76.4 \).