Arccosine Calculator
Enter a cosine value to calculate the corresponding angle in both degrees and radians.
Calculate arccos(x)
Degrees
Radians
What is the Arccosine Function?
The arccosine function, also called the inverse cosine function, is the reverse of the cosine function. It is represented as \(\arccos(x)\) or \(\cos^{-1}(x)\). This function is used to determine the angle corresponding to a specific cosine value. For the cosine function \(y = \cos(\theta)\), the arccosine is defined as: \( \theta = \arccos(x) \) Here: \(-1 \leq x \leq 1\), \(0 \leq \theta \leq \pi\). The range of the arccosine function is \([0, \pi]\), ensuring it is unique and invertible.
Examples
Example 1: Find the angle for \(\cos(\theta) = 0\)
Solution:
\( \theta = \arccos(0) = \frac{\pi}{2} \approx 1.5708 \, \text{radians} \)
The angle corresponding to a cosine value of 0 is \(\frac{\pi}{2}\) or 90°.
Example 2: Find the angle for \(\cos(\theta) = 0.5\)
Solution:
\( \theta = \arccos(0.5) = \frac{\pi}{3} \approx 1.0472 \, \text{radians} \)
The angle corresponding to a cosine value of 0.5 is \(\frac{\pi}{3}\) or 60°.
Graph of the Arccosine Function
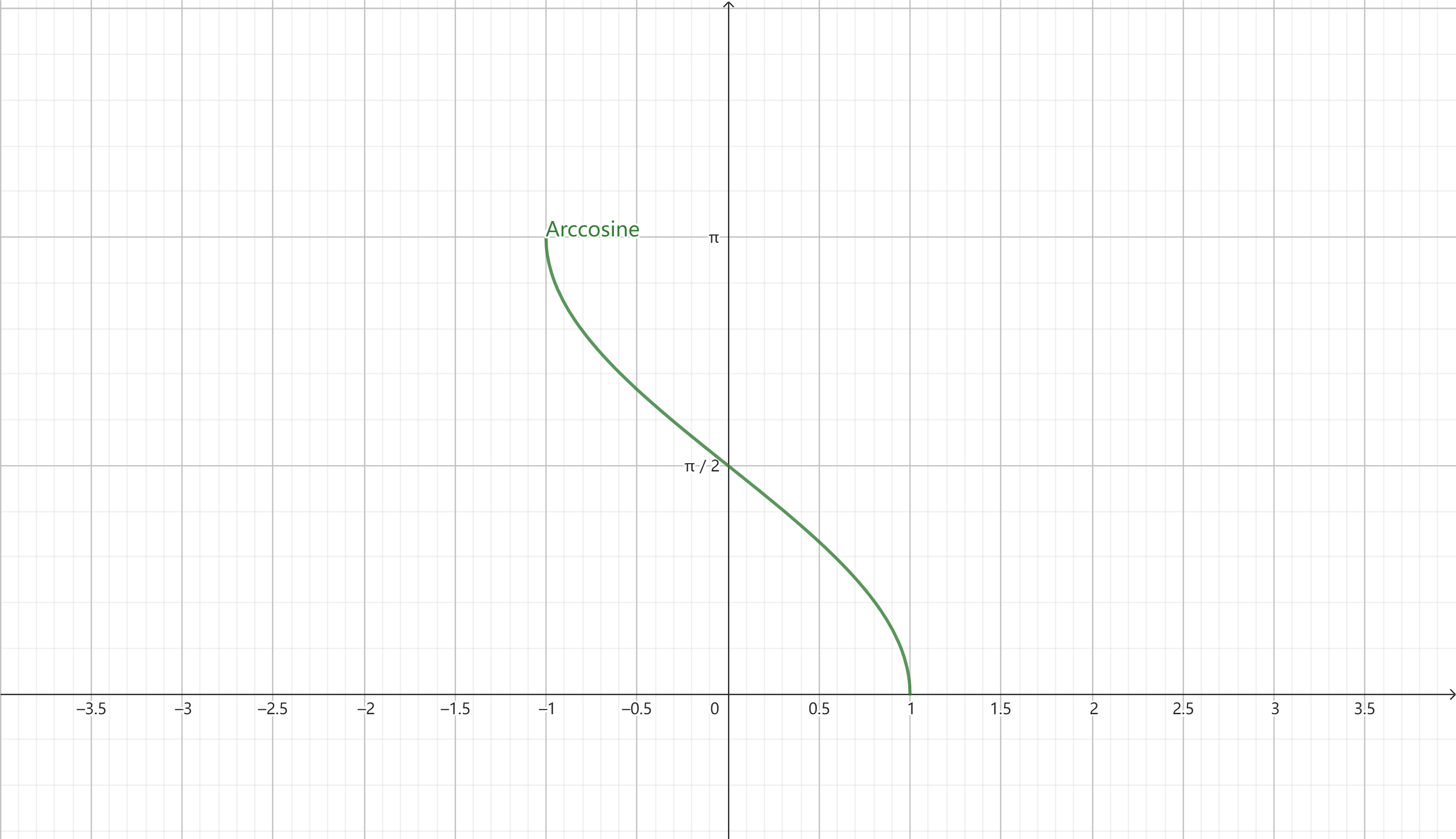
The graph of the arccosine function is a smooth, decreasing curve, starting at \((1, 0)\) and ending at \((-1, \pi)\). Below are its key characteristics:
- Domain: \([-1, 1]\)
- Range: \([0, \pi]\)
- Monotonicity: The arccosine function is strictly decreasing across its domain.
- Parity: The arccosine function does not exhibit odd or even symmetry.
Arccosine Conversion Table
| Cosine Value | Degrees | Radians |
|---|---|---|
| 1 | 0° | 0 |
| 0.9998477 | 1° | \(\frac{\pi}{180}\) |
| 0.99939083 | 2° | \(\frac{\pi}{90}\) |
| 0.99862953 | 3° | \(\frac{\pi}{60}\) |
| 0.99756405 | 4° | \(\frac{\pi}{45}\) |
| 0.9961947 | 5° | \(\frac{\pi}{36}\) |
| 0.9945219 | 6° | \(\frac{\pi}{30}\) |
| 0.99254615 | 7° | \(\frac{7\pi}{180}\) |
| 0.99026807 | 8° | \(\frac{2\pi}{45}\) |
| 0.98768834 | 9° | \(\frac{\pi}{20}\) |
| 0.98480775 | 10° | \(\frac{\pi}{18}\) |
| 0.98162718 | 11° | \(\frac{11\pi}{180}\) |
| 0.9781476 | 12° | \(\frac{\pi}{15}\) |
| 0.97437006 | 13° | \(\frac{13\pi}{180}\) |
| 0.97029573 | 14° | \(\frac{7\pi}{90}\) |
| 0.96592583 | 15° | \(\frac{\pi}{12}\) |
| 0.9612617 | 16° | \(\frac{4\pi}{45}\) |
| 0.95630476 | 17° | \(\frac{17\pi}{180}\) |
| 0.95105652 | 18° | \(\frac{\pi}{10}\) |
| 0.94551858 | 19° | \(\frac{19\pi}{180}\) |
| 0.93969262 | 20° | \(\frac{\pi}{9}\) |
| 0.93358043 | 21° | \(\frac{7\pi}{60}\) |
| 0.92718385 | 22° | \(\frac{11\pi}{90}\) |
| 0.92050485 | 23° | \(\frac{23\pi}{180}\) |
| 0.91354546 | 24° | \(\frac{2\pi}{15}\) |
| 0.90630779 | 25° | \(\frac{5\pi}{36}\) |
| 0.89879405 | 26° | \(\frac{13\pi}{90}\) |
| 0.89100652 | 27° | \(\frac{3\pi}{20}\) |
| 0.88294759 | 28° | \(\frac{7\pi}{45}\) |
| 0.87461971 | 29° | \(\frac{29\pi}{180}\) |
| 0.8660254 | 30° | \(\frac{\pi}{6}\) |
| 0.8571673 | 31° | \(\frac{31\pi}{180}\) |
| 0.8480481 | 32° | \(\frac{8\pi}{45}\) |
| 0.83867057 | 33° | \(\frac{11\pi}{60}\) |
| 0.82903757 | 34° | \(\frac{17\pi}{90}\) |
| 0.81915204 | 35° | \(\frac{7\pi}{36}\) |
| 0.80901699 | 36° | \(\frac{\pi}{5}\) |
| 0.79863551 | 37° | \(\frac{37\pi}{180}\) |
| 0.78801075 | 38° | \(\frac{19\pi}{90}\) |
| 0.77714596 | 39° | \(\frac{13\pi}{60}\) |
| 0.76604444 | 40° | \(\frac{2\pi}{9}\) |
| 0.75470958 | 41° | \(\frac{41\pi}{180}\) |
| 0.74314483 | 42° | \(\frac{7\pi}{30}\) |
| 0.7313537 | 43° | \(\frac{43\pi}{180}\) |
| 0.7193398 | 44° | \(\frac{11\pi}{45}\) |
| 0.70710678 | 45° | \(\frac{\pi}{4}\) |
| 0.69465837 | 46° | \(\frac{23\pi}{90}\) |
| 0.68199836 | 47° | \(\frac{47\pi}{180}\) |
| 0.66913061 | 48° | \(\frac{4\pi}{15}\) |
| 0.65605903 | 49° | \(\frac{49\pi}{180}\) |
| 0.64278761 | 50° | \(\frac{5\pi}{18}\) |
| 0.62932039 | 51° | \(\frac{17\pi}{60}\) |
| 0.61566148 | 52° | \(\frac{13\pi}{45}\) |
| 0.60181502 | 53° | \(\frac{53\pi}{180}\) |
| 0.58778525 | 54° | \(\frac{3\pi}{10}\) |
| 0.57357644 | 55° | \(\frac{11\pi}{36}\) |
| 0.5591929 | 56° | \(\frac{14\pi}{45}\) |
| 0.54463904 | 57° | \(\frac{19\pi}{60}\) |
| 0.52991926 | 58° | \(\frac{29\pi}{90}\) |
| 0.51503807 | 59° | \(\frac{59\pi}{180}\) |
| 0.5 | 60° | \(\frac{\pi}{3}\) |
| 0.48480962 | 61° | \(\frac{61\pi}{180}\) |
| 0.46947156 | 62° | \(\frac{31\pi}{90}\) |
| 0.4539905 | 63° | \(\frac{7\pi}{20}\) |
| 0.43837115 | 64° | \(\frac{16\pi}{45}\) |
| 0.42261826 | 65° | \(\frac{13\pi}{36}\) |
| 0.40673664 | 66° | \(\frac{11\pi}{30}\) |
| 0.39073113 | 67° | \(\frac{67\pi}{180}\) |
| 0.37460659 | 68° | \(\frac{17\pi}{45}\) |
| 0.35836795 | 69° | \(\frac{23\pi}{60}\) |
| 0.34202014 | 70° | \(\frac{7\pi}{18}\) |
| 0.32556815 | 71° | \(\frac{71\pi}{180}\) |
| 0.30901699 | 72° | \(\frac{2\pi}{5}\) |
| 0.2923717 | 73° | \(\frac{73\pi}{180}\) |
| 0.27563736 | 74° | \(\frac{37\pi}{90}\) |
| 0.25881905 | 75° | \(\frac{5\pi}{12}\) |
| 0.2419219 | 76° | \(\frac{19\pi}{45}\) |
| 0.22495105 | 77° | \(\frac{77\pi}{180}\) |
| 0.20791169 | 78° | \(\frac{13\pi}{30}\) |
| 0.190809 | 79° | \(\frac{79\pi}{180}\) |
| 0.17364818 | 80° | \(\frac{4\pi}{9}\) |
| 0.15643447 | 81° | \(\frac{9\pi}{20}\) |
| 0.1391731 | 82° | \(\frac{41\pi}{90}\) |
| 0.12186934 | 83° | \(\frac{83\pi}{180}\) |
| 0.10452846 | 84° | \(\frac{7\pi}{15}\) |
| 0.08715574 | 85° | \(\frac{17\pi}{36}\) |
| 0.06975647 | 86° | \(\frac{43\pi}{90}\) |
| 0.05233596 | 87° | \(\frac{29\pi}{60}\) |
| 0.0348995 | 88° | \(\frac{22\pi}{45}\) |
| 0.01745241 | 89° | \(\frac{89\pi}{180}\) |
| 0 | 90° | \(\frac{\pi}{2}\) |
| -0.01745241 | 91° | \(\frac{91\pi}{180}\) |
| -0.0348995 | 92° | \(\frac{23\pi}{45}\) |
| -0.05233596 | 93° | \(\frac{31\pi}{60}\) |
| -0.06975647 | 94° | \(\frac{47\pi}{90}\) |
| -0.08715574 | 95° | \(\frac{19\pi}{36}\) |
| -0.10452846 | 96° | \(\frac{8\pi}{15}\) |
| -0.12186934 | 97° | \(\frac{97\pi}{180}\) |
| -0.1391731 | 98° | \(\frac{49\pi}{90}\) |
| -0.15643447 | 99° | \(\frac{11\pi}{20}\) |
| -0.17364818 | 100° | \(\frac{5\pi}{9}\) |
| -0.190809 | 101° | \(\frac{101\pi}{180}\) |
| -0.20791169 | 102° | \(\frac{17\pi}{30}\) |
| -0.22495105 | 103° | \(\frac{103\pi}{180}\) |
| -0.2419219 | 104° | \(\frac{26\pi}{45}\) |
| -0.25881905 | 105° | \(\frac{7\pi}{12}\) |
| -0.27563736 | 106° | \(\frac{53\pi}{90}\) |
| -0.2923717 | 107° | \(\frac{107\pi}{180}\) |
| -0.30901699 | 108° | \(\frac{3\pi}{5}\) |
| -0.32556815 | 109° | \(\frac{109\pi}{180}\) |
| -0.34202014 | 110° | \(\frac{11\pi}{18}\) |
| -0.35836795 | 111° | \(\frac{37\pi}{60}\) |
| -0.37460659 | 112° | \(\frac{28\pi}{45}\) |
| -0.39073113 | 113° | \(\frac{113\pi}{180}\) |
| -0.40673664 | 114° | \(\frac{19\pi}{30}\) |
| -0.42261826 | 115° | \(\frac{23\pi}{36}\) |
| -0.43837115 | 116° | \(\frac{29\pi}{45}\) |
| -0.4539905 | 117° | \(\frac{13\pi}{20}\) |
| -0.46947156 | 118° | \(\frac{59\pi}{90}\) |
| -0.48480962 | 119° | \(\frac{119\pi}{180}\) |
| -0.5 | 120° | \(\frac{2\pi}{3}\) |
| -0.51503807 | 121° | \(\frac{121\pi}{180}\) |
| -0.52991926 | 122° | \(\frac{61\pi}{90}\) |
| -0.54463904 | 123° | \(\frac{41\pi}{60}\) |
| -0.5591929 | 124° | \(\frac{31\pi}{45}\) |
| -0.57357644 | 125° | \(\frac{25\pi}{36}\) |
| -0.58778525 | 126° | \(\frac{7\pi}{10}\) |
| -0.60181502 | 127° | \(\frac{127\pi}{180}\) |
| -0.61566148 | 128° | \(\frac{32\pi}{45}\) |
| -0.62932039 | 129° | \(\frac{43\pi}{60}\) |
| -0.64278761 | 130° | \(\frac{13\pi}{18}\) |
| -0.65605903 | 131° | \(\frac{131\pi}{180}\) |
| -0.66913061 | 132° | \(\frac{11\pi}{15}\) |
| -0.68199836 | 133° | \(\frac{133\pi}{180}\) |
| -0.69465837 | 134° | \(\frac{67\pi}{90}\) |
| -0.70710678 | 135° | \(\frac{3\pi}{4}\) |
| -0.7193398 | 136° | \(\frac{34\pi}{45}\) |
| -0.7313537 | 137° | \(\frac{137\pi}{180}\) |
| -0.74314483 | 138° | \(\frac{23\pi}{30}\) |
| -0.75470958 | 139° | \(\frac{139\pi}{180}\) |
| -0.76604444 | 140° | \(\frac{7\pi}{9}\) |
| -0.77714596 | 141° | \(\frac{47\pi}{60}\) |
| -0.78801075 | 142° | \(\frac{71\pi}{90}\) |
| -0.79863551 | 143° | \(\frac{143\pi}{180}\) |
| -0.80901699 | 144° | \(\frac{4\pi}{5}\) |
| -0.81915204 | 145° | \(\frac{29\pi}{36}\) |
| -0.82903757 | 146° | \(\frac{73\pi}{90}\) |
| -0.83867057 | 147° | \(\frac{49\pi}{60}\) |
| -0.8480481 | 148° | \(\frac{37\pi}{45}\) |
| -0.8571673 | 149° | \(\frac{149\pi}{180}\) |
| -0.8660254 | 150° | \(\frac{5\pi}{6}\) |
| -0.87461971 | 151° | \(\frac{151\pi}{180}\) |
| -0.88294759 | 152° | \(\frac{38\pi}{45}\) |
| -0.89100652 | 153° | \(\frac{17\pi}{20}\) |
| -0.89879405 | 154° | \(\frac{77\pi}{90}\) |
| -0.90630779 | 155° | \(\frac{31\pi}{36}\) |
| -0.91354546 | 156° | \(\frac{13\pi}{15}\) |
| -0.92050485 | 157° | \(\frac{157\pi}{180}\) |
| -0.92718385 | 158° | \(\frac{79\pi}{90}\) |
| -0.93358043 | 159° | \(\frac{53\pi}{60}\) |
| -0.93969262 | 160° | \(\frac{8\pi}{9}\) |
| -0.94551858 | 161° | \(\frac{161\pi}{180}\) |
| -0.95105652 | 162° | \(\frac{9\pi}{10}\) |
| -0.95630476 | 163° | \(\frac{163\pi}{180}\) |
| -0.9612617 | 164° | \(\frac{41\pi}{45}\) |
| -0.96592583 | 165° | \(\frac{11\pi}{12}\) |
| -0.97029573 | 166° | \(\frac{83\pi}{90}\) |
| -0.97437006 | 167° | \(\frac{167\pi}{180}\) |
| -0.9781476 | 168° | \(\frac{14\pi}{15}\) |
| -0.98162718 | 169° | \(\frac{169\pi}{180}\) |
| -0.98480775 | 170° | \(\frac{17\pi}{18}\) |
| -0.98768834 | 171° | \(\frac{19\pi}{20}\) |
| -0.99026807 | 172° | \(\frac{43\pi}{45}\) |
| -0.99254615 | 173° | \(\frac{173\pi}{180}\) |
| -0.9945219 | 174° | \(\frac{29\pi}{30}\) |
| -0.9961947 | 175° | \(\frac{35\pi}{36}\) |
| -0.99756405 | 176° | \(\frac{44\pi}{45}\) |
| -0.99862953 | 177° | \(\frac{59\pi}{60}\) |
| -0.99939083 | 178° | \(\frac{89\pi}{90}\) |
| -0.9998477 | 179° | \(\frac{179\pi}{180}\) |
| -1 | 180° | π |