Midpoint Calculator

Enter two coordinates to calculate the midpoint between them in just a few seconds.

Calculate the Midpoint

The First Point

The Second Point

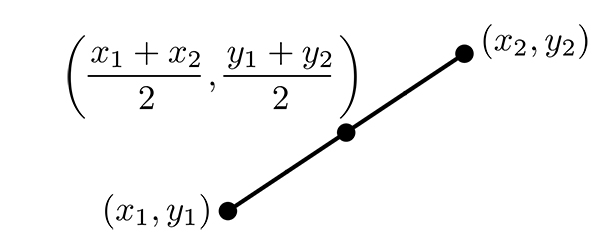
Midpoint

What Is a Midpoint?

In geometry, the midpoint is the central point of a line segment connecting two points. For given coordinates \( (x_1, y_1) \) and \( (x_2, y_2) \), the midpoint \( M \) is the average of the two points' x- and y-coordinates.

How to Calculate a Midpoint

For two points \( (x_1, y_1) \) and \( (x_2, y_2) \). The x-coordinate of the midpoint is: \( x = \frac{x_1 + x_2}{2} \) The y-coordinate of the midpoint is: \( y = \frac{y_1 + y_2}{2} \) Thus, the midpoint \( M(x, y) \) is: \( M = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) \)

Examples

Example 1: Two Points \( A(2, 3) \) and \( B(8, 7) \), find the Midpoint \( M \).

Solution:

\( x = \frac{2 + 8}{2} = 5 \)

\( y = \frac{3 + 7}{2} = 5 \)

Result: Midpoint \( M(5, 5) \)

Example 2: Two Points \( C(-4, 6) \) and \( D(10, -2) \), find the Midpoint \( M \).

Solution:

\( x = \frac{-4 + 10}{2} = 3 \)

\( y = \frac{6 + (-2)}{2} = 2 \)

Result: Midpoint \( M(3, 2) \)