Regular Polygon Calculator
Entering the number of sides and a known property value (side length, perimeter, area, apothem, inradius, or circumradius) to quickly calculate other geometric parameters of a regular polygon.
Calculate the Perimeter, Area, Inradius, Circumradius, Apothem, and Other Properties of a Regular Polygon
Side Length
Perimeter
Area
Apothem
Inradius
Circumradius
Interior Angle
Sum of Interior Angles
Sum of Exterior Angles
What is a Regular Polygon?
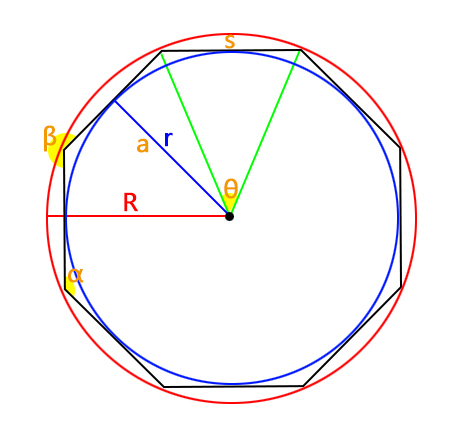
A regular polygon is a polygon with all sides of equal length and all interior angles equal. Common examples include the equilateral triangle, square, and regular pentagon. The geometric properties of a regular polygon, such as side length, perimeter, area, apothem, inradius, circumradius, interior angles, sum of interior angles, and sum of exterior angles, can be calculated from the number of sides and one known property.
How to Calculate the Properties of a Regular Polygon?
Let nn be the number of sides and ss the side length of the regular polygon. The formulas to calculate its properties are:
Perimeter
The perimeter of a regular polygon is the sum of all its sides: \( P = n \times s \)
Area
The area of the polygon's enclosed region is given by: \( A = \frac{n \times s^2}{4 \times \tan\left(\frac{\pi}{n}\right)} \) Alternatively, it can be calculated using the perimeter and apothem: \( A = \frac{1}{2} \times Perimeter \times Apothem \)
Inradius (Apothem)
The inradius is the radius of the inscribed circle, also known as the apothem: \( r = \frac{s}{2 \times \tan\left(\frac{\pi}{n}\right)} \)
Circumradius
The circumradius is the radius of the circumscribed circle, which is the distance from the center to any vertex: \( R = \frac{s}{2 \times \sin\left(\frac{\pi}{n}\right)} \)
Apothem
The apothem is the perpendicular distance from the center of the regular polygon to one of its sides: \( A_p = \frac{s}{2 \times \tan\left(\frac{\pi}{n}\right)} \)
Interior Angle
The angle formed by two adjacent sides of the regular polygon: \( \text{Angle}_{\text{int}} = \frac{(n - 2) \times 180^\circ}{n} \)
Sum of Interior Angles
The sum of all interior angles of the regular polygon: \( \text{Angle Sum}_{\text{int}} = (n - 2) \times 180^\circ \)
Sum of Exterior Angles
The sum of all exterior angles of a regular polygon is always 360°.
Example: Given n = 6 sides and side length s = 4, calculate the perimeter, area, inradius, circumradius, and interior angle of a regular hexagon.
Solution:
Perimeter:
\( P = n \times s = 6 \times 4 = 24 \)
Area:
\( A = \frac{6 \times 4^2}{4 \times \tan\left(\frac{\pi}{6}\right)} = \frac{6 \times 16}{4 \times \frac{\sqrt{3}}{3}} \approx 41.57 \)
Inradius (Apothem):
\( r = \frac{4}{2 \times \tan\left(\frac{\pi}{6}\right)} = \frac{4}{2 \times \frac{\sqrt{3}}{3}} \approx 3.46 \)
Circumradius:
\( R = \frac{4}{2 \times \sin\left(\frac{\pi}{6}\right)} = \frac{4}{2 \times \frac{1}{2}} = 4 \)
Interior Angle:
\( \text{Angle}_{\text{int}} = \frac{(6 - 2) \times 180^\circ}{6} = \frac{720^\circ}{6} = 120^\circ \)