Semicircle Calculator
Enter a known attribute of the semicircle (such as radius, arc length, circumference, or area) to calculate the other three attributes.
Calculate the Radius, Arc Length, Circumference, and Area of a Semicircle
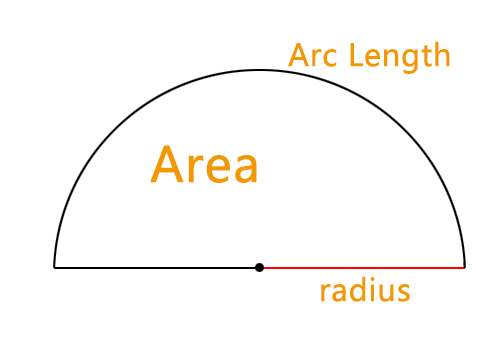
Radius
Arc Length
Circumference
Area
What is a Semicircle?
A semicircle is half of a circle, with similar geometric properties. The calculation of a semicircle involves attributes such as the radius, arc length, circumference, and area. Given one known attribute, the other three can be calculated.
How to Calculate the Properties of a Semicircle?
You can calculate other properties of the semicircle based on a known attribute. The specific formulas are as follows:
Given the Radius (r):
Calculate the Arc Length: \( L = \pi r \) Calculate the Circumference: \( P = 2r + \pi r = (2 + \pi)r \) Calculate the Area: \( A = \frac{1}{2} \pi r^2 \)
Given the Arc Length (L):
Calculate the Radius: \( r = \frac{L}{\pi} \) Calculate the Circumference: \( P = L + 2r = L + 2 \times \frac{L}{\pi} \) Calculate the Area: \( A = \frac{L^2}{2 \pi} \)
Given the Circumference (P):
Calculate the Radius: \( r = \frac{P}{2 + \pi} \) Calculate the Arc Length: \( L = \frac{P \pi}{2 + \pi} \) Calculate the Area: \( A = \frac{P^2 \pi}{2(\pi + 2)^2} \)
Given the Area (A):
Calculate the Radius: \( r = \sqrt{\frac{2A}{\pi}} \) Calculate the Arc Length: \( L = \pi r = \sqrt{2A\pi} \) Calculate the Circumference: \( P = (2 + \pi)r = (2 + \pi)\sqrt{\frac{2A}{\pi}} \)
Examples
Example 1: Given the radius of the semicircle as 5, calculate the arc length, circumference, and area.
Solution:
Arc Length:
\( L = πr = π × 5 ≈ 15.71 \)
Circumference:
\( P = (2 + π)r = (2 + π) × 5 ≈ 25.708 \)
Area:
\( A= \frac{1}{2} \pi r^2 = \frac{1}{2} \pi \times 5^2 \approx 39.27 \)
Result: The arc length is approximately 15.71, the circumference is approximately 25.71, and the area is approximately 39.27.
Example 2: Given the area of the semicircle as 50, calculate the radius, arc length, and circumference.
Solution:
Radius:
\( r = \sqrt{\frac{2A}{\pi}} = \sqrt{\frac{2 \times 50}{\pi}} \approx 5.64 \)
Arc Length:
\( L = πr = π × 5.64 ≈ 17.72 \)
Circumference:
\( P = (2 + π)r = (2 + π) × 5.64 ≈ 29.01 \)
Result: The radius is approximately 5.64, the arc length is approximately 17.72, and the circumference is approximately 29.01.