Sine Calculator
Enter an angle in degrees or radians to calculate the sine value quickly.
Calculate Sin(θ)
Result
Definition of Sine Function
The sine function is one of the fundamental trigonometric functions widely used in mathematics, physics, and engineering. It is commonly represented as \(\sin(\theta)\), where \(\theta\) is the angle, often measured in radians.
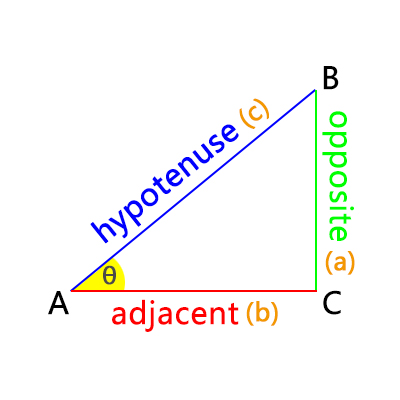
In a right triangle, the sine of an acute angle is the ratio of the length of the side opposite the angle to the hypotenuse. If \(\theta\) is the angle, \(a\) is the opposite side, and \(c\) is the hypotenuse, the sine is calculated as: \( \sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{a}{c} \)
Sine can also be defined geometrically using the unit circle, a circle with a radius of 1 centered at the origin of a coordinate plane. For an angle \(\theta\), the \(y\)-coordinate of the corresponding point on the circle is the sine value: \( \sin(\theta) = y \)
How to Calculate Sine Values
Example 1: Calculating Sine in a Triangle
In a right triangle with \(\theta = 30^\circ\), an opposite side of length 3, and a hypotenuse of length 6: \( \sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{3}{6} = 0.5 \) Thus, the sine of \(30^\circ\) is 0.5.
Example 2: Practical Application
You're standing on top of a 50-meter tower and observing a point on the ground at a \(45^\circ\) angle. To find the distance to the point: \( \sin(45^\circ) = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{50}{\text{Distance}} \) Since \(\sin(45^\circ) = \frac{\sqrt{2}}{2} \approx 0.707\): \( \text{Distance} = \frac{50}{0.707} \approx 70.71 \, \text{meters} \) The distance to the point is approximately 70.71 meters.
Sine Function Graph and Properties
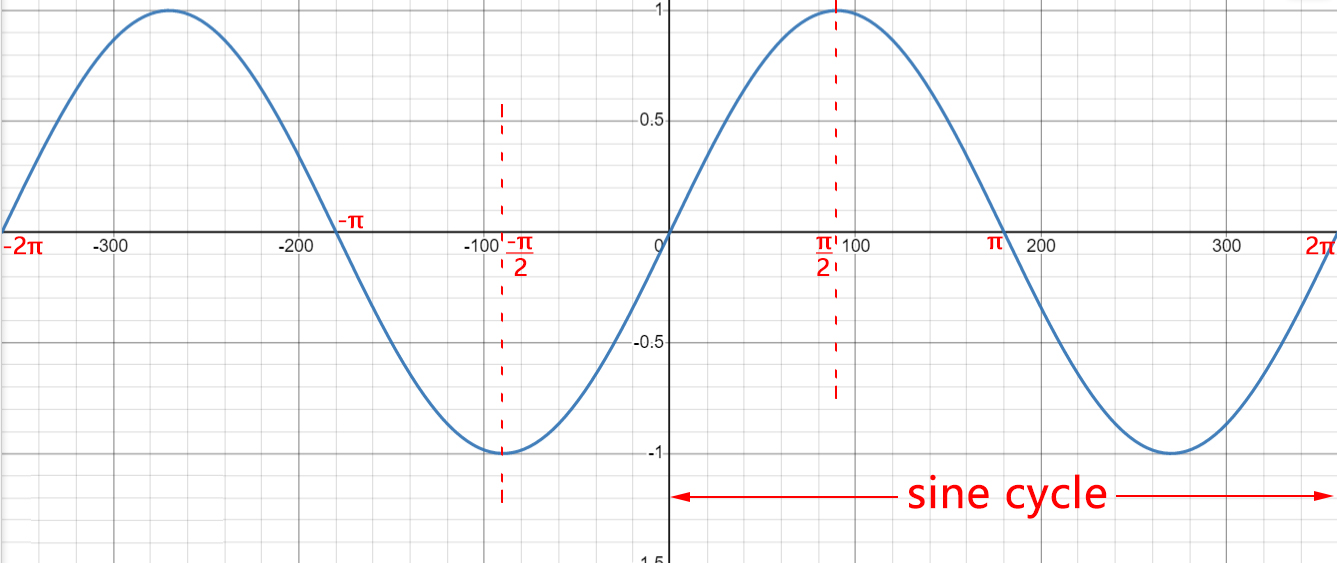
The sine function is periodic and forms a smooth wave, commonly called the sine wave. It describes oscillatory behavior in various fields, such as sound, light, and electromagnetic waves.
- Periodicity: The sine function repeats every \(2\pi\) radians or 360°: \( \sin(\theta + 2\pi) = \sin(\theta) \)
- Symmetry: The sine function is symmetric about the origin, making it an odd function: \(\sin(-\theta) = -\sin(\theta)\).
- Amplitude: The amplitude (maximum deviation from zero) is 1.
- Wave Peaks and Valleys: Peaks occur at \(\theta = \frac{\pi}{2} + 2n\pi\) (\(\sin(\theta) = 1\)). Valleys occur at \(\theta = \frac{3\pi}{2} + 2n\pi\) (\(\sin(\theta) = -1\)).
- Domain and Range: The domain of the sine function is all real numbers \(\mathbb{R}\). The sine function oscillates between \(-1\) and \(1\).
Quadrant Characteristics of the Sine Function
The sine function's behavior varies across the four quadrants:
| Quadrant | Degrees | Radians | Sign | Range | Monotonicity |
|---|---|---|---|---|---|
| First Quadrant | \(0^\circ\) - \(90^\circ\) | \(0\) - \(\frac{\pi}{2}\) | Positive | \((0, 1]\) | Increasing |
| Second Quadrant | \(90^\circ\) - \(180^\circ\) | \(\frac{\pi}{2}\) - \(\pi\) | Positive | \([1, 0)\) | Decreasing |
| Third Quadrant | \(180^\circ\) - \(270^\circ\) | \(\pi\) - \(\frac{3\pi}{2}\) | Negative | \((0, -1]\) | Decreasing |
| Fourth Quadrant | \(270^\circ\) - \(360^\circ\) | \(\frac{3\pi}{2}\) - \(2\pi\) | Negative | \([-1, 0)\) | Increasing |
Other Sine Calculations
1. Reciprocal Function (Cosecant)
The reciprocal of sine is the cosecant function (\(\csc(\theta)\)): \( \frac{1}{\sin(\theta)} = \csc(\theta) \) Note: Undefined when \(\sin(\theta) = 0\).
2. Derivative of Sine
The derivative of \(\sin(\theta)\) is the cosine function \(\cos(\theta)\): \( \frac{d}{d\theta} \sin(\theta) = \cos(\theta) \)
3. Integral of Sine
The integral of \(\sin(\theta)\) is: \( \int \sin(\theta) \, d\theta = -\cos(\theta) + C \)
4. Inverse Sine (Arcsine)
The arcsine function (\(\arcsin(x)\)) finds the angle corresponding to a given sine value. It is defined for \([-1, 1]\): \( \theta = \arcsin(x) \)
Common Sine Values Table
| Degree | Radian | Sine Value |
|---|---|---|
| 0° | 0 | 0 |
| 5° | \(\frac{\pi}{36}\) | 0.08715574 |
| 10° | \(\frac{\pi}{18}\) | 0.17364818 |
| 15° | \(\frac{\pi}{12}\) | 0.25881905 |
| 20° | \(\frac{\pi}{9}\) | 0.34202014 |
| 25° | \(\frac{5\pi}{36}\) | 0.42261826 |
| 30° | \(\frac{\pi}{6}\) | 0.5 |
| 35° | \(\frac{7\pi}{36}\) | 0.57357644 |
| 40° | \(\frac{2\pi}{9}\) | 0.64278761 |
| 45° | \(\frac{\pi}{4}\) | 0.70710678 |
| 50° | \(\frac{5\pi}{18}\) | 0.76604444 |
| 55° | \(\frac{11\pi}{36}\) | 0.81915204 |
| 60° | \(\frac{\pi}{3}\) | 0.8660254 |
| 65° | \(\frac{13\pi}{36}\) | 0.90630779 |
| 70° | \(\frac{7\pi}{18}\) | 0.93969262 |
| 75° | \(\frac{5\pi}{12}\) | 0.96592583 |
| 80° | \(\frac{4\pi}{9}\) | 0.98480775 |
| 85° | \(\frac{17\pi}{36}\) | 0.9961947 |
| 90° | \(\frac{\pi}{2}\) | 1 |
| 95° | \(\frac{19\pi}{36}\) | 0.9961947 |
| 100° | \(\frac{5\pi}{9}\) | 0.98480775 |
| 105° | \(\frac{7\pi}{12}\) | 0.96592583 |
| 110° | \(\frac{11\pi}{18}\) | 0.93969262 |
| 115° | \(\frac{23\pi}{36}\) | 0.90630779 |
| 120° | \(\frac{2\pi}{3}\) | 0.8660254 |
| 125° | \(\frac{25\pi}{36}\) | 0.81915204 |
| 130° | \(\frac{13\pi}{18}\) | 0.76604444 |
| 135° | \(\frac{3\pi}{4}\) | 0.70710678 |
| 140° | \(\frac{7\pi}{9}\) | 0.64278761 |
| 145° | \(\frac{29\pi}{36}\) | 0.57357644 |
| 150° | \(\frac{5\pi}{6}\) | 0.5 |
| 155° | \(\frac{31\pi}{36}\) | 0.42261826 |
| 160° | \(\frac{8\pi}{9}\) | 0.34202014 |
| 165° | \(\frac{11\pi}{12}\) | 0.25881905 |
| 170° | \(\frac{17\pi}{18}\) | 0.17364818 |
| 175° | \(\frac{35\pi}{36}\) | 0.08715574 |
| 180° | π | 0 |
| 185° | \(\frac{37\pi}{36}\) | -0.08715574 |
| 190° | \(\frac{19\pi}{18}\) | -0.17364818 |
| 195° | \(\frac{13\pi}{12}\) | -0.25881905 |
| 200° | \(\frac{10\pi}{9}\) | -0.34202014 |
| 205° | \(\frac{41\pi}{36}\) | -0.42261826 |
| 210° | \(\frac{7\pi}{6}\) | -0.5 |
| 215° | \(\frac{43\pi}{36}\) | -0.57357644 |
| 220° | \(\frac{11\pi}{9}\) | -0.64278761 |
| 225° | \(\frac{5\pi}{4}\) | -0.70710678 |
| 230° | \(\frac{23\pi}{18}\) | -0.76604444 |
| 235° | \(\frac{47\pi}{36}\) | -0.81915204 |
| 240° | \(\frac{4\pi}{3}\) | -0.8660254 |
| 245° | \(\frac{49\pi}{36}\) | -0.90630779 |
| 250° | \(\frac{25\pi}{18}\) | -0.93969262 |
| 255° | \(\frac{17\pi}{12}\) | -0.96592583 |
| 260° | \(\frac{13\pi}{9}\) | -0.98480775 |
| 265° | \(\frac{53\pi}{36}\) | -0.9961947 |
| 270° | \(\frac{3\pi}{2}\) | -1 |
| 275° | \(\frac{55\pi}{36}\) | -0.9961947 |
| 280° | \(\frac{14\pi}{9}\) | -0.98480775 |
| 285° | \(\frac{19\pi}{12}\) | -0.96592583 |
| 290° | \(\frac{29\pi}{18}\) | -0.93969262 |
| 295° | \(\frac{59\pi}{36}\) | -0.90630779 |
| 300° | \(\frac{5\pi}{3}\) | -0.8660254 |
| 305° | \(\frac{61\pi}{36}\) | -0.81915204 |
| 310° | \(\frac{31\pi}{18}\) | -0.76604444 |
| 315° | \(\frac{7\pi}{4}\) | -0.70710678 |
| 320° | \(\frac{16\pi}{9}\) | -0.64278761 |
| 325° | \(\frac{65\pi}{36}\) | -0.57357644 |
| 330° | \(\frac{11\pi}{6}\) | -0.5 |
| 335° | \(\frac{67\pi}{36}\) | -0.42261826 |
| 340° | \(\frac{17\pi}{9}\) | -0.34202014 |
| 345° | \(\frac{23\pi}{12}\) | -0.25881905 |
| 350° | \(\frac{35\pi}{18}\) | -0.17364818 |
| 355° | \(\frac{71\pi}{36}\) | -0.08715574 |
| 360° | 2π | 0 |