Tangent Calculator
Input an angle in degrees or radians to calculate the corresponding tangent value.
Calculate tan(θ)
Result
Definition and Formula of Tangent
The tangent function, denoted as \(\tan(\theta)\), is a fundamental trigonometric function used to describe the relationship between an angle and the sides of a right triangle. The angle \(\theta\) is usually measured in radians.
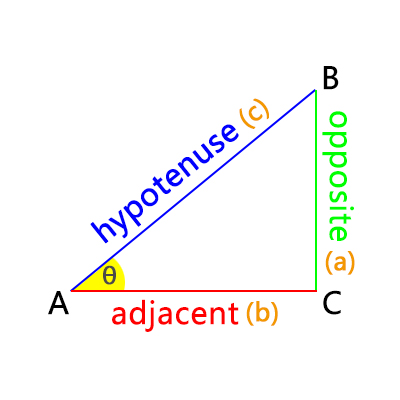
In a right triangle, the tangent of an angle \(\theta\) is defined as the ratio of the opposite side to the adjacent side: \( \tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{a}{b} \) This represents the vertical to horizontal component ratio of the angle.
On the unit circle, the tangent function is defined as the ratio of the y-coordinate to the x-coordinate of the point corresponding to the angle \(\theta\): \( \tan(\theta) = \frac{y}{x} \) Here, \(x\) and \(y\) are the coordinates of the point on the unit circle.
Examples
Example 1: Calculating Tangent Using a Right Triangle
A right triangle has one acute angle \(\theta = 45^\circ\), with the opposite side measuring 4 units and the adjacent side measuring 4 units. Calculate the tangent of this angle.
Solution:
Using the definition of tangent:
\( \tan(45^\circ) = \frac{4}{4} = 1 \)
Thus, \(\tan(45^\circ) = 1\).
Example 2: Tangent in Practical Applications
You observe a tower that is 30 meters tall from a horizontal distance of 40 meters. Calculate the angle \(\theta\) between your line of sight and the ground.
Solution:
Using the tangent definition:
\( \tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{30}{40} = 0.75 \)
Using the inverse tangent function:
\( \theta = \arctan(0.75) \approx 36.87^\circ \)
The angle is approximately \(36.87^\circ\).
Properties and Graph of Tangent
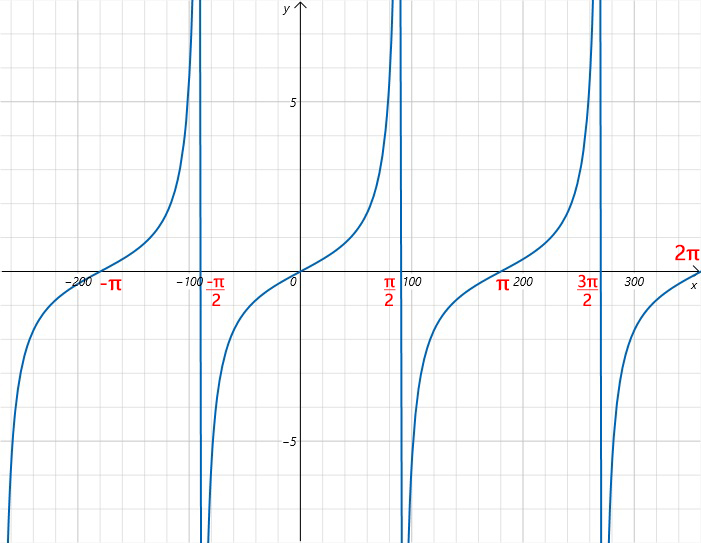
Key Characteristics:
- Periodicity: The tangent function repeats every \(\pi\) radians (\(180^\circ\)), \(\tan(\theta + n\pi) = \tan(\theta)\), where \(n\) is an integer.
- Monotonicity: The tangent function is monotonically increasing within each period.
- Odd Function: Tangent satisfies \(\tan(-\theta) = -\tan(\theta)\), meaning it is symmetric about the origin.
- Amplitude: The tangent function has no amplitude limit, as its range is all real numbers (\(\mathbb{R}\)).
- Asymptotes: Vertical asymptotes occur at \(\theta = \frac{\pi}{2} + n\pi\), where \(n\) is an integer.
- Domain and Range: The domain of the tangent function is all angles \(\theta\) (except \(\frac{\pi}{2} + n\pi\)), and the range is \(\mathbb{R}\) (all real numbers).
Quadrant Properties
The tangent function's sign varies by quadrant:
| Quadrant | Degrees | Radians | Sign | Range | Monotonicity |
|---|---|---|---|---|---|
| 1st Quadrant | \(0^\circ\) - \(90^\circ\) | \(0\) - \(\frac{\pi}{2}\) | Positive | \((0, \infty)\) | Increasing |
| 2nd Quadrant | \(90^\circ\) - \(180^\circ\) | \(\frac{\pi}{2}\) - \(\pi\) | Negative | \((-\infty, 0)\) | Increasing |
| 3rd Quadrant | \(180^\circ\) - \(270^\circ\) | \(\pi\) - \(\frac{3\pi}{2}\) | Positive | \((0, \infty)\) | Increasing |
| 4th Quadrant | \(270^\circ\) - \(360^\circ\) | \(\frac{3\pi}{2}\) - \(2\pi\) | Negative | \((-\infty, 0)\) | Increasing |
Additional Tangent Calculations
1. Reciprocal of Tangent (Cotangent)
The reciprocal of tangent is the cotangent function: \( \frac{1}{\tan(\theta)} = \cot(\theta) = \frac{\text{Adjacent}}{\text{Opposite}} \) Undefined when \(\tan(\theta) = 0\).
2. Derivative of Tangent
The derivative of \(\tan(\theta)\) is the square of the secant function: \( \frac{d}{d\theta} \tan(\theta) = \sec^2(\theta) \) This property is useful in calculus for analyzing rate changes.
3. Integral of Tangent
The integral of \(\tan(\theta)\) is given by: \( \int \tan(\theta) \, d\theta = -\ln|\cos(\theta)| + C \) This integral is frequently used in physics and engineering.
4. Inverse Tangent (arctan)
The arctangent function computes the angle corresponding to a tangent value. Its domain is all real numbers, and its range is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\): \( \theta = \arctan(x) \)
Common Tangent Values
| Degree | Radian | Tangent Value |
|---|---|---|
| 0° | 0 | 0.0 |
| 5° | \(\frac{\pi}{36}\) | 0.08748866 |
| 10° | \(\frac{\pi}{18}\) | 0.17632698 |
| 15° | \(\frac{\pi}{12}\) | 0.26794919 |
| 20° | \(\frac{\pi}{9}\) | 0.36397023 |
| 25° | \(\frac{5\pi}{36}\) | 0.46630766 |
| 30° | \(\frac{\pi}{6}\) | 0.57735027 |
| 35° | \(\frac{7\pi}{36}\) | 0.70020754 |
| 40° | \(\frac{2\pi}{9}\) | 0.83909963 |
| 45° | \(\frac{\pi}{4}\) | 1 |
| 50° | \(\frac{5\pi}{18}\) | 1.19175359 |
| 55° | \(\frac{11\pi}{36}\) | 1.42814801 |
| 60° | \(\frac{\pi}{3}\) | 1.73205081 |
| 65° | \(\frac{13\pi}{36}\) | 2.14450692 |
| 70° | \(\frac{7\pi}{18}\) | 2.74747742 |
| 75° | \(\frac{5\pi}{12}\) | 3.73205081 |
| 80° | \(\frac{4\pi}{9}\) | 5.67128182 |
| 85° | \(\frac{17\pi}{36}\) | 11.4300523 |
| 95° | \(\frac{19\pi}{36}\) | -11.4300523 |
| 100° | \(\frac{5\pi}{9}\) | -5.67128182 |
| 105° | \(\frac{7\pi}{12}\) | -3.73205081 |
| 110° | \(\frac{11\pi}{18}\) | -2.74747742 |
| 115° | \(\frac{23\pi}{36}\) | -2.14450692 |
| 120° | \(\frac{2\pi}{3}\) | -1.73205081 |
| 125° | \(\frac{25\pi}{36}\) | -1.42814801 |
| 130° | \(\frac{13\pi}{18}\) | -1.19175359 |
| 135° | \(\frac{3\pi}{4}\) | -1 |
| 140° | \(\frac{7\pi}{9}\) | -0.83909963 |
| 145° | \(\frac{29\pi}{36}\) | -0.70020754 |
| 150° | \(\frac{5\pi}{6}\) | -0.57735027 |
| 155° | \(\frac{31\pi}{36}\) | -0.46630766 |
| 160° | \(\frac{8\pi}{9}\) | -0.36397023 |
| 165° | \(\frac{11\pi}{12}\) | -0.26794919 |
| 170° | \(\frac{17\pi}{18}\) | -0.17632698 |
| 175° | \(\frac{35\pi}{36}\) | -0.08748866 |
| 180° | π | 0 |
| 185° | \(\frac{37\pi}{36}\) | 0.08748866 |
| 190° | \(\frac{19\pi}{18}\) | 0.17632698 |
| 195° | \(\frac{13\pi}{12}\) | 0.26794919 |
| 200° | \(\frac{10\pi}{9}\) | 0.36397023 |
| 205° | \(\frac{41\pi}{36}\) | 0.46630766 |
| 210° | \(\frac{7\pi}{6}\) | 0.57735027 |
| 215° | \(\frac{43\pi}{36}\) | 0.70020754 |
| 220° | \(\frac{11\pi}{9}\) | 0.83909963 |
| 225° | \(\frac{5\pi}{4}\) | 1 |
| 230° | \(\frac{23\pi}{18}\) | 1.19175359 |
| 235° | \(\frac{47\pi}{36}\) | 1.42814801 |
| 240° | \(\frac{4\pi}{3}\) | 1.73205081 |
| 245° | \(\frac{49\pi}{36}\) | 2.14450692 |
| 250° | \(\frac{25\pi}{18}\) | 2.74747742 |
| 255° | \(\frac{17\pi}{12}\) | 3.73205081 |
| 260° | \(\frac{13\pi}{9}\) | 5.67128182 |
| 265° | \(\frac{53\pi}{36}\) | 11.4300523 |
| 275° | \(\frac{55\pi}{36}\) | -11.4300523 |
| 280° | \(\frac{14\pi}{9}\) | -5.67128182 |
| 285° | \(\frac{19\pi}{12}\) | -3.73205081 |
| 290° | \(\frac{29\pi}{18}\) | -2.74747742 |
| 295° | \(\frac{59\pi}{36}\) | -2.14450692 |
| 300° | \(\frac{5\pi}{3}\) | -1.73205081 |
| 305° | \(\frac{61\pi}{36}\) | -1.42814801 |
| 310° | \(\frac{31\pi}{18}\) | -1.19175359 |
| 315° | \(\frac{7\pi}{4}\) | -1 |
| 320° | \(\frac{16\pi}{9}\) | -0.83909963 |
| 325° | \(\frac{65\pi}{36}\) | -0.70020754 |
| 330° | \(\frac{11\pi}{6}\) | -0.57735027 |
| 335° | \(\frac{67\pi}{36}\) | -0.46630766 |
| 340° | \(\frac{17\pi}{9}\) | -0.36397023 |
| 345° | \(\frac{23\pi}{12}\) | -0.26794919 |
| 350° | \(\frac{35\pi}{18}\) | -0.17632698 |
| 355° | \(\frac{71\pi}{36}\) | -0.08748866 |
| 360° | 2π | 0 |