Triangular Number Calculator

What is a Triangular Number?

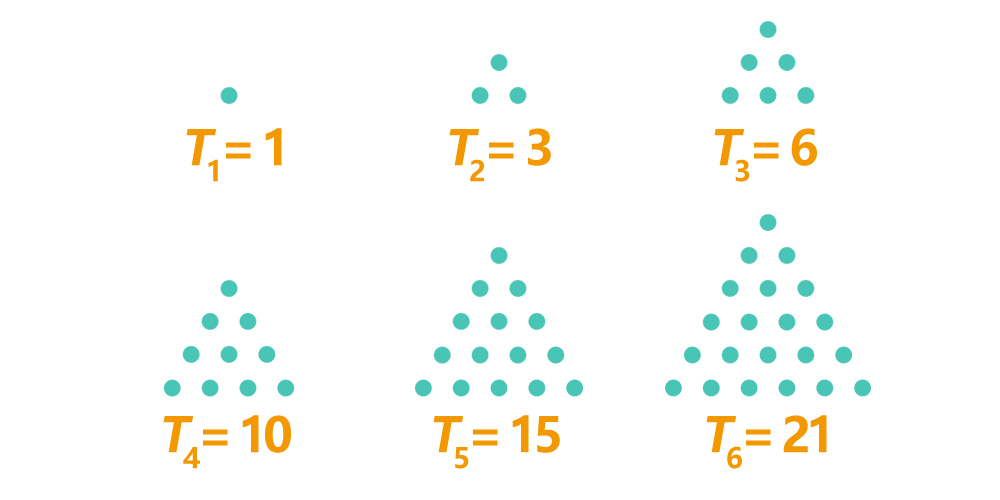
A triangular number represents a number that can form an equilateral triangle using dots. The \(n\)-th triangular number can be calculated using the formula: \( T_n = \frac{n(n + 1)}{2} \) where \(n\) is a positive integer.

How to Determine if a Number is a Triangular Number

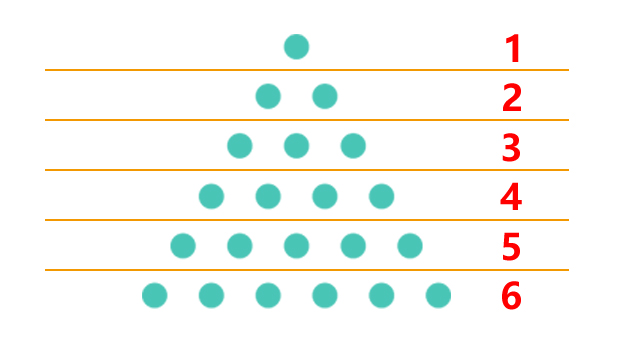
A number \(x\) is triangular if there exists a positive integer \(n\) such that: \( x = \frac{n(n + 1)}{2} \) This means the total number of dots in the sequence matches the sum of an arithmetic series starting at 1 with a common difference of 1.

Calculation Steps:

1. For a given \(x\), solve the equation \(n(n + 1) = 2x\).
2. Rewrite the equation as: \(n^2 + n - 2x = 0\).
3. Use the quadratic formula: \(n = \frac{-1 \pm \sqrt{1 + 8x}}{2}\), If \(n\) is a positive integer, \(x\) is a triangular number.

Examples

Example 1: Is 10 a Triangular Number?

Example 2: Is 36 a Triangular Number?

Example 3: Is 150 a Triangular Number?

First 100 Triangular Numbers