圓心角計算器

什麼是圓心角？

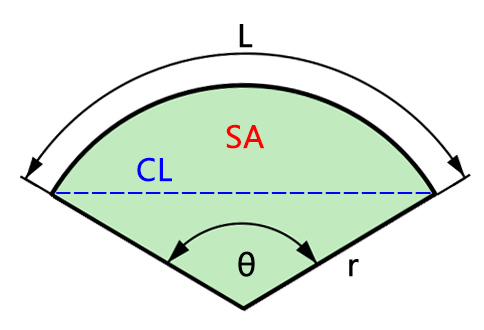
圓心角是從圓心出發形成的夾角，用於描述扇形的範圍大小。在已知扇形的半徑 \(r \) 以及弧長、弦長或面積之一的情況下，可以計算出圓心角 \(\theta \)。

如何計算圓心角？

假設已知半徑 \( r \) 和以下任一值來求圓心角：

已知弧長 \( L \)

若要求角度 \( \theta \) 為度數，則： \( \theta = \frac{360 \times L}{2 \pi r} \) 若要求角度 \( \theta \) 為弧度，則： \( \theta = \frac{L}{r} \)

已知弦長 \( c \)

首先將弦長公式重組： \( \theta = 2 \times \arcsin\left(\frac{c}{2r}\right) \) 若需要度數輸出，可將弧度結果轉換為度數 \( \theta \times \frac{180}{\pi} \)。

已知面積 \( A \)

若面積公式中角度 \( \theta \) 為度數： \( \theta = \frac{360 \times A}{\pi r^2} \) 若角度為弧度，則： \( \theta = \frac{2A}{r^2} \)

示例

例子 1：已知半徑 \(r = 8 \) 且弧長 \(l = 12 \)，求圓心角。

例子 2：已知半徑 \(r = 10 \) 且扇形面積 \(a = 40 \)，求圓心角。