弓形計算器
輸入弓形的圓心角(度數或弧度)和一個已知屬性值(如半徑、弦長、弧長、面積等),快速計算弓形的其它幾何屬性。
計算弓形的半徑、弦長、弧長、周長、面積、高度等
半徑
弦長
弧長
高度
周長
面積
什麼是弓形?
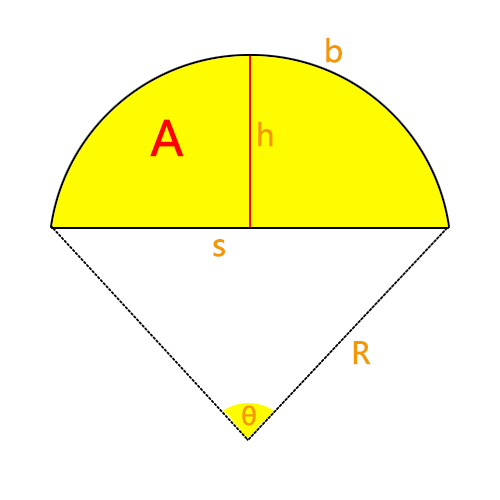
弓形是由圓的弧和該弧所對應的弦所圍成的區域,它是由一個圓心角(度數或弧度)以及弧長、弦長、高度、周長或面積等屬性描述的幾何形狀。
如何計算弓形的屬性?
假設弓形對應的圓心角為 θ(以弧度為單位),半徑是 r。
弦長
弦長是連接圓上兩個點的直線距離,公式為: \( \text{Chord Length} = 2 \times r \times \sin\left(\frac{\theta}{2}\right) \)
弧長
弧長是圓弧的長度,可以通過以下公式計算: \( \text{Arc Length} = \theta \times r \)
高度
高度是弓形的頂點到弦的垂直距離,公式是: \( h = r - \sqrt{r^2 - \left(\frac{\text{Chord Length}}{2}\right)^2} \) 其中,Chord Length 是弦長。
周長
弓形的周長是弧長與弦長之和: \( P = \text{Arc Length} + \text{Chord Length} \)
面積
弓形的面積是由圓心角對應的扇形面積減去三角形面積: \( A = \frac{1}{2} r^2 (\theta - \sin\theta) \)
示例:已知圓心角 θ = 60°,半徑 r = 10,計算弓形的弦長、弧長、高度、周長和麵積。
解答:
角度轉為弧度:
\( \theta = 60^\circ = \frac{60 \times \pi}{180} = \frac{\pi}{3} \text{ rad} \)
弦長:
\( \text{Chord Length} = 2 \times 10 \times \sin\left(\frac{\pi}{6}\right) = 20 \times \frac{1}{2} = 10 \)
弧長:
\( \text{Arc Length} = \theta \times r = \frac{\pi}{3} \times 10 \approx 10.47 \)
高度:
\( h = 10 - \sqrt{10^2 - \left(\frac{10}{2}\right)^2} = 10 - \sqrt{100 - 25} \approx 1.34 \)
周長:
\( P = \text{Arc Length} + \text{Chord Length} = 10.47 + 10 = 20.47 \)
面積:
\( A = \frac{1}{2} \times 10^2 \times \left(\frac{\pi}{3} - \sin\left(\frac{\pi}{3}\right)\right) \approx 9.06 \)