橢圓計算器
輸入半長軸和半短軸,快速計算橢圓的周長、面積和離心率。
計算橢圓的周長、面積和離心率
周長
面積
離心率
什麼是橢圓?
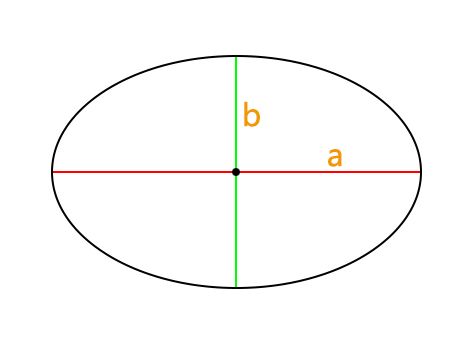
橢圓是平面上與一個焦點及兩條定焦線的距離之和保持恆定的點的軌跡。橢圓的兩條軸分別是半長軸和半短軸。半長軸是橢圓沿最長方向的半徑,而半短軸是橢圓沿最短方向的半徑。橢圓的周長、面積和離心率等可以通過已知的半長軸和半短軸來計算。
如何計算橢圓周長?
由於橢圓周長的精確計算公式是非常複雜的,通常使用近似公式: \( P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \) 其中:a 為半長軸,b 為半短軸。
如何計算橢圓面積?
橢圓的面積計算公式為: \( A = \pi a b \) 其中:a 為半長軸,b 為半短軸。
如何計算橢圓離心率?
離心率 e 表示橢圓的扁平程度,計算公式為: \( e = \sqrt{1 - \frac{b^2}{a^2}} \) 同樣,a 為半長軸,b 為半短軸。
示例
例子 1:已知橢圓的半長軸為 6,半短軸為 4,計算橢圓的周長、面積和離心率。
解答:
計算周長:
\( P \approx \pi \left[ 3(6 + 4) - \sqrt{(3 \times 6 + 4)(6 + 3 \times 4)} \right] \approx 31.73 \)
計算面積:
\( A = \pi \times 6 \times 4 = 24\pi \approx 75.398 \)
計算離心率:
\( e = \sqrt{1 - \frac{4^2}{6^2}} \approx 0.745 \)
例子 2:已知橢圓的半長軸為 10,半短軸為 6,計算橢圓的周長、面積和離心率。
解答:
計算周長:
\( P \approx \pi \left[ 3(10 + 6) - \sqrt{(3 \times 10 + 6)(10 + 3 \times 6)} \right] \approx 51.054 \)
計算面積:
\( A = \pi \times 10 \times 6 = 60\pi \approx 188.496 \)
計算離心率:
\( e = \sqrt{1 - \frac{6^2}{10^2}} = \sqrt{0.64} = 0.8 \)