黃金比例計算器

什麼是黃金比例？

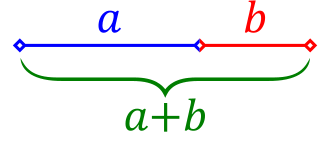
黃金比例是一種特殊的比例關係，通常表示為： \( \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \) 在長度分割中，若總長為 \( L \)，且分成兩部分 \( a \) 和 \( b \)，則滿足： \( \frac{L}{a} = \frac{a}{b} = \phi \) 在此比例中，\( a \) 被稱為較長部分，\( b \) 為較短部分。

如何計算黃金比例缺失部分

假設已知部分長度 \( a \) 或總長度 \( L \)，則可以通過以下方法計算：

• 已知較長部分 \( a \)：計算較短部分 \( b = \frac{a}{\phi} \) 和總長度 \( L = a + b \)。
• 已知較短部分 \( b \)：計算較長部分 \( a = b \times \phi \) 和總長度 \( L = a + b \)。
• 已知總長度 \( L \)：計算較長部分 \( a = \frac{L}{\phi + 1} \) 和較短部分 \( b = L - a \)。

示例

例子 1：已知較長部分 \( a = 100 \)，計算較短部分 \( b \) 和總長度 \( L \)。

例子 2：已知總長度 \( L = 200 \)，計算較長部分 \( a \) 和較短部分 \( b \)。