長方形計算器

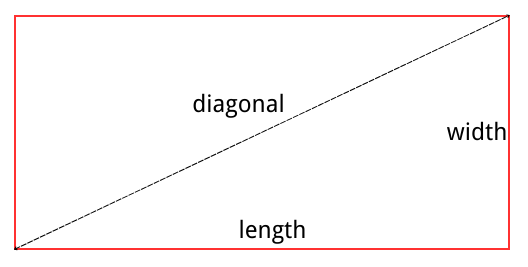
長方形的基本屬性

長方形的屬性包括長 \( l \)、寬 \( w \)、周長 \( P \)、面積 \( A \) 和對角線 \( d \)。它們之間有以下關係：

周長與長、寬的關係： \( P = 2l + 2w \)

面積與長、寬的關係： \( A = l \times w \)

對角線與長、寬的關係： \( d = \sqrt{l^2 + w^2} \)

只要知道長方形的任意兩個屬性，就可以根據這些公式推算出長方形的其它屬性。

如何計算長方形的相關屬性

假設你已知長方形的兩個參數，以下是根據已知參數計算其它三個參數的方式：

已知長 \( l \) 和寬 \( w \)

• 計算周長：\( P = 2l + 2w \)
• 計算面積：\( A = l \times w \)
• 計算對角線：\( d = \sqrt{l^2 + w^2} \)

已知長 \( l \) 和周長 \( P \)

• 計算寬：\( w = \frac{P}{2} - l \)
• 計算面積：\( A = l \times w \)
• 計算對角線：\( d = \sqrt{l^2 + w^2} \)

已知長 \( l \) 和面積 \( A \)

• 計算寬：\( w = \frac{A}{l} \)
• 計算周長：\( P = 2l + 2w \)
• 計算對角線：\( d = \sqrt{l^2 + w^2} \)

已知長 \( l \) 和對角線 \( d \)

• 計算寬：\( w = \sqrt{d^2 - l^2} \)
• 計算周長：\( P = 2l + 2w \)
• 計算面積：\( A = l \times w \)

若已知寬 \( w \)，把上述公式中，長 \( l \) 替換成寬 \( w \) 即可。

已知周長 \( P \) 和面積 \( A \)

根據長方形的周長公式 \( P = 2l + 2w \) 和面積公式 \( A = l \times w \) 可構建二次方程，接著利用求根公式來求解 \( l \) 和 \( w \)。

已知周長 \( P \) 和對角線 \( d \)

• 使用周長公式 \( P = 2l + 2w \) 和對角線公式 \( d = \sqrt{l^2 + w^2} \)。
• 利用這兩個方程，可以解出 \( l \) 和 \( w \)。

已知面積 \( A \) 和對角線 \( d \)

• 使用面積公式 \( A = l \times w \) 和對角線公式 \( d = \sqrt{l^2 + w^2} \)。
• 利用這兩個方程，可解出 \( l \) 和 \( w \)。

示例

例子 1：已知長方形的長 \( l = 8 \) 和寬 \( w = 6 \)，求周長、面積和對角線。

例子 2：已知長方形的周長 \( P = 28 \) 和面積 \( A = 48 \)，求長、寬和對角線。

例子 3：已知周長 \( P = 28 \) 和對角線 \( d = 10 \)，求長和寬。

例子 4：已知面積 \( A = 48 \) 和對角線 \( d = 10 \)，求長和寬。