正方形計算器
輸入正方形的一個參數(邊長、周長、面積或對角線),計算正方形的邊長、周長、面積和對角線。
正方形邊長、周長、面積和對角線計算
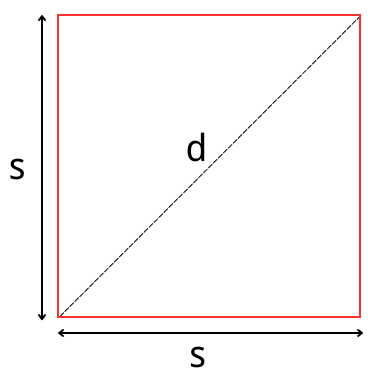
邊長
周長
面積
對角線
正方形的基本屬性
正方形的所有邊長相等,且其四個角為直角。正方形的屬性之間有以下基本關係:
周長與邊長的關係: \( \text{周長} = 4 \times \text{邊長} \)
面積與邊長的關係: \( \text{面積} = \text{邊長}^2 \)
對角線與邊長的關係: \( \text{對角線} = \text{邊長} \times \sqrt{2} \)
若要計算正方形的其它屬性,可根據這三個公式進行演變。
如何計算正方形的相關屬性
假設你已知正方形的某一參數,以下是根據已知參數計算正方形其它三個屬性的方式:
已知邊長 \( a \)
- 計算周長:\( C = 4a \)
- 計算面積:\( A = a^2 \)
- 計算對角線:\( d = a \sqrt{2} \)
已知周長 \( C \)
- 計算邊長:\( a = \frac{C}{4} \)
- 計算面積:\( A = \left(\frac{C}{4}\right)^2 \)
- 計算對角線:\( d = \frac{C}{4} \times \sqrt{2} \)
已知面積 \( A \)
- 計算邊長:\( a = \sqrt{A} \)
- 計算周長:\( C = 4 \times \sqrt{A} \)
- 計算對角線:\( d = \sqrt{A} \times \sqrt{2} \)
已知對角線 \( d \)
- 計算邊長:\( a = \frac{d}{\sqrt{2}} \)
- 計算周長:\( C = \frac{d}{\sqrt{2}} \times 4 \)
- 計算面積:\( A = \left(\frac{d}{\sqrt{2}}\right)^2 \)
示例
例子 1:已知正方形的邊長 \( a = 6 \),求周長、面積和對角線。
解答:
計算周長:
\( C = 4 \times 6 = 24 \)
計算面積:
\( A = 6^2 = 36 \)
計算對角線:
\( d = 6 \times \sqrt{2} \approx 8.49 \)
結果:周長為 24,面積為 36,對角線約為 8.49。
例子 2:已知正方形的周長 \( C = 20 \),求邊長、面積和對角線。
解答:
計算邊長:
\( a = \frac{20}{4} = 5 \)
計算面積:
\( A = 5^2 = 25 \)
計算對角線:
\( d = 5 \times \sqrt{2} \approx 7.07 \)
結果:邊長為 5,面積為 25,對角線約為 7.07。
例子 3:已知正方形的面積 \( A = 144 \),求邊長、周長和對角線。
解答:
計算邊長:
\( a = \sqrt{144} = 12 \)
計算周長:
\( C = 4 \times 12 = 48 \)
計算對角線:
\( d = 12 \times \sqrt{2} \approx 16.97 \)
結果:邊長為 12,周長為 48,對角線約為 16.97。