正切計算器
輸入角度或弧度,計算對應的正切值。
正切計算
結果
正切的定義和公式
正切函數(Tangent function)是三角函數中的一種,常用於描述角度與直角三角形邊長的關係。它通常用符號 \(\tan(\theta)\) 表示,其中 \(\theta\) 是角度,通常以弧度為單位。

在直角三角形中,正切函數定義為角度 \(\theta\) 的 對邊與 鄰邊 之比,公式為: \( \tan(\theta) = \frac{\text{對邊}}{\text{鄰邊}} = \frac{a}{b} \) 即正切函數表示一個角度的垂直與水平分量之比。
在單位圓中,正切函數定義為單位圓上對應角度 \(\theta\) 的點的縱座標與橫座標的比值: \( \tan(\theta) = \frac{y}{x} \) 其中,\(x\) 和 \(y\) 是單位圓上與角度 \(\theta\) 對應點的橫縱座標。
示例
例子 1:通過直角三角形計算正切值
假設有一個直角三角形,其中一個銳角 \(\theta = 45^\circ\),對邊的長度為 4,鄰邊的長度為 4,求這個角的正切值。
解答:
根據正切的定義:
\( \tan(45^\circ) = \frac{4}{4} = 1 \)
因此,角度 \(45^\circ\) 的正切值是 1。
例子 2:實際應用中的正切值計算
假設你正在觀察一座 30 米高的塔樓,並且你與塔樓的水平距離為 40 米,要求你與塔樓之間的角度 \(\theta\)。
解答:
根據正切的定義:
\( \tan(\theta) = \frac{\text{對邊}}{\text{鄰邊}} = \frac{30}{40} = 0.75 \)
使用反正切函數(\(\arctan\))可以求得:
\( \theta = \arctan(0.75) \approx 36.87^\circ \)
因此,角度 \(\theta \approx 36.87^\circ\)。
正切圖形和特性
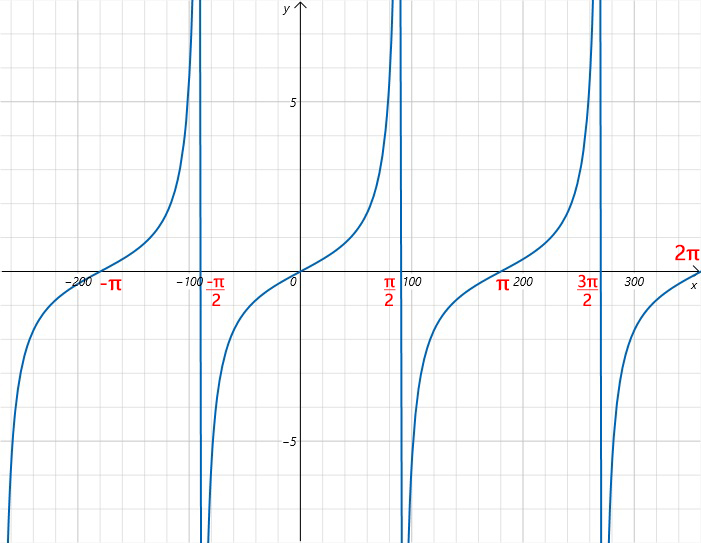
正切函數的圖形呈現出周期性的波動,並且在每個周期中有豎直漸近線。正切圖形具有以下特性:
- 周期性:正切函數的周期為 \(\pi\)(即 180°),即每 \(\pi\) 弧度圖形重複一次。
- 單調性:正切函數在每個周期內是單調遞增的。
- 奇函數:正切函數是奇函數,即 \(\tan(-\theta) = -\tan(\theta)\),這意味著正切函數關於原點對稱。
- 振幅:正切函數的振幅是無限的,正切值可以從負無窮大增長到正無窮大。
- 漸近線:在 \(\theta = \frac{\pi}{2} + n\pi\) 處(其中 \(n\) 是整數),正切函數有豎直漸近線,即函數值趨向於無窮大或負無窮大。
- 定義域和值域:正切函數的定義域是所有角度 \(\theta\)(除了 \(\frac{\pi}{2} + n\pi\)),值域為 \(\mathbb{R}\)(所有實數)。
正切函數的象限特性(Quadrant Properties)
正切函數在不同象限中的符號和性質如下表所示:
| 象限 | 角度 | 弧度 | 值符號 | 值範圍 | 單調性 |
|---|---|---|---|---|---|
| 第一象限 | \(0^\circ\) - \(90^\circ\) | \(0\) - \(\frac{\pi}{2}\) | + | \((0, \infty)\) | 遞增 |
| 第二象限 | \(90^\circ\) - \(180^\circ\) | \(\frac{\pi}{2}\) - \(\pi\) | - | \((-\infty, 0)\) | 遞增 |
| 第三象限 | \(180^\circ\) - \(270^\circ\) | \(\pi\) - \(\frac{3\pi}{2}\) | + | \((0, \infty)\) | 遞增 |
| 第四象限 | \(270^\circ\) - \(360^\circ\) | \(\frac{3\pi}{2}\) - \(2\pi\) | - | \((-\infty, 0)\) | 遞增 |
- 在第一象限,正切值為正,且隨著角度的增加從 0 增加到正無窮大。
- 在第二象限,正切值為負,且隨著角度的增加從負無窮大增加到 0。
- 在第三象限,正切值為正,且隨著角度的增加從 0 增加到正無窮大。
- 在第四象限,正切值為負,且隨著角度的增加從負無窮大增加到 0。
正切的其它計算
1. 正切的倒數(餘切函數)
正切函數的倒數是餘切函數(cotangent,記作 \(\cot(\theta)\)),定義為: \( \frac{1}{\tan(\theta)} = \cot(\theta) = \frac{\text{鄰邊}}{\text{對邊}} \) 當 \(\tan(\theta) = 0\) 時,餘切函數無定義。
2. 正切的導數
正切函數的導數是正割函數的平方,即: \( \frac{d}{d\theta} \tan(\theta) = \sec^2(\theta) \) 這一性質在微積分中非常重要,尤其是在解析函數變化率時。
3. 正切的積分
正切函數的積分是對數函數: \( \int \tan(\theta) \, d\theta = -\ln|\cos(\theta)| + C \) 這一積分常常出現在物理學中的振動、波動分析等應用中。
4. 反正切函數(arctan)
反正切函數(arctangent,記作 \(\arctan(x)\))用於求解給定正切值對應的角度。反正切函數的定義域為所有實數,值域為 \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\),即: \( \theta = \arctan(x) \) 其中 \(x\) 為正切值。
正切常用值表
| 角度 | 弧度 | 正切值 |
|---|---|---|
| 0° | 0 | 0.0 |
| 5° | \(\frac{\pi}{36}\) | 0.08748866 |
| 10° | \(\frac{\pi}{18}\) | 0.17632698 |
| 15° | \(\frac{\pi}{12}\) | 0.26794919 |
| 20° | \(\frac{\pi}{9}\) | 0.36397023 |
| 25° | \(\frac{5\pi}{36}\) | 0.46630766 |
| 30° | \(\frac{\pi}{6}\) | 0.57735027 |
| 35° | \(\frac{7\pi}{36}\) | 0.70020754 |
| 40° | \(\frac{2\pi}{9}\) | 0.83909963 |
| 45° | \(\frac{\pi}{4}\) | 1 |
| 50° | \(\frac{5\pi}{18}\) | 1.19175359 |
| 55° | \(\frac{11\pi}{36}\) | 1.42814801 |
| 60° | \(\frac{\pi}{3}\) | 1.73205081 |
| 65° | \(\frac{13\pi}{36}\) | 2.14450692 |
| 70° | \(\frac{7\pi}{18}\) | 2.74747742 |
| 75° | \(\frac{5\pi}{12}\) | 3.73205081 |
| 80° | \(\frac{4\pi}{9}\) | 5.67128182 |
| 85° | \(\frac{17\pi}{36}\) | 11.4300523 |
| 95° | \(\frac{19\pi}{36}\) | -11.4300523 |
| 100° | \(\frac{5\pi}{9}\) | -5.67128182 |
| 105° | \(\frac{7\pi}{12}\) | -3.73205081 |
| 110° | \(\frac{11\pi}{18}\) | -2.74747742 |
| 115° | \(\frac{23\pi}{36}\) | -2.14450692 |
| 120° | \(\frac{2\pi}{3}\) | -1.73205081 |
| 125° | \(\frac{25\pi}{36}\) | -1.42814801 |
| 130° | \(\frac{13\pi}{18}\) | -1.19175359 |
| 135° | \(\frac{3\pi}{4}\) | -1 |
| 140° | \(\frac{7\pi}{9}\) | -0.83909963 |
| 145° | \(\frac{29\pi}{36}\) | -0.70020754 |
| 150° | \(\frac{5\pi}{6}\) | -0.57735027 |
| 155° | \(\frac{31\pi}{36}\) | -0.46630766 |
| 160° | \(\frac{8\pi}{9}\) | -0.36397023 |
| 165° | \(\frac{11\pi}{12}\) | -0.26794919 |
| 170° | \(\frac{17\pi}{18}\) | -0.17632698 |
| 175° | \(\frac{35\pi}{36}\) | -0.08748866 |
| 180° | π | 0 |
| 185° | \(\frac{37\pi}{36}\) | 0.08748866 |
| 190° | \(\frac{19\pi}{18}\) | 0.17632698 |
| 195° | \(\frac{13\pi}{12}\) | 0.26794919 |
| 200° | \(\frac{10\pi}{9}\) | 0.36397023 |
| 205° | \(\frac{41\pi}{36}\) | 0.46630766 |
| 210° | \(\frac{7\pi}{6}\) | 0.57735027 |
| 215° | \(\frac{43\pi}{36}\) | 0.70020754 |
| 220° | \(\frac{11\pi}{9}\) | 0.83909963 |
| 225° | \(\frac{5\pi}{4}\) | 1 |
| 230° | \(\frac{23\pi}{18}\) | 1.19175359 |
| 235° | \(\frac{47\pi}{36}\) | 1.42814801 |
| 240° | \(\frac{4\pi}{3}\) | 1.73205081 |
| 245° | \(\frac{49\pi}{36}\) | 2.14450692 |
| 250° | \(\frac{25\pi}{18}\) | 2.74747742 |
| 255° | \(\frac{17\pi}{12}\) | 3.73205081 |
| 260° | \(\frac{13\pi}{9}\) | 5.67128182 |
| 265° | \(\frac{53\pi}{36}\) | 11.4300523 |
| 275° | \(\frac{55\pi}{36}\) | -11.4300523 |
| 280° | \(\frac{14\pi}{9}\) | -5.67128182 |
| 285° | \(\frac{19\pi}{12}\) | -3.73205081 |
| 290° | \(\frac{29\pi}{18}\) | -2.74747742 |
| 295° | \(\frac{59\pi}{36}\) | -2.14450692 |
| 300° | \(\frac{5\pi}{3}\) | -1.73205081 |
| 305° | \(\frac{61\pi}{36}\) | -1.42814801 |
| 310° | \(\frac{31\pi}{18}\) | -1.19175359 |
| 315° | \(\frac{7\pi}{4}\) | -1 |
| 320° | \(\frac{16\pi}{9}\) | -0.83909963 |
| 325° | \(\frac{65\pi}{36}\) | -0.70020754 |
| 330° | \(\frac{11\pi}{6}\) | -0.57735027 |
| 335° | \(\frac{67\pi}{36}\) | -0.46630766 |
| 340° | \(\frac{17\pi}{9}\) | -0.36397023 |
| 345° | \(\frac{23\pi}{12}\) | -0.26794919 |
| 350° | \(\frac{35\pi}{18}\) | -0.17632698 |
| 355° | \(\frac{71\pi}{36}\) | -0.08748866 |
| 360° | 2π | 0 |