反正割计算器
输入正割值,计算对应的角度和弧度。
反正割计算
角度
弧度
什么是反正割函数
反正割函数(Arcsecant function)是正割函数的反函数,通常用符号 \(\operatorname{arcsec}(x)\) 或 \(\sec^{-1}(x)\) 表示,用于计算给定正割值对应的角度。对于正割函数 \(y = \sec(\theta)\),反正割函数定义为: \( \theta = \operatorname{arcsec}(x) \) 其中,\(x \leq -1\) 或 \(x \geq 1\),而角度 \(\theta\) 的值域为 \([0, \pi]\) 且 \(\theta \neq \frac{\pi}{2}\)。这样定义确保反正割函数的唯一性和可逆性。
示例
例子 1:假设已知 \(\sec(\theta) = 2\),求对应的角度 \(\theta\):
解答:
\( \theta = \operatorname{arcsec}(2) \approx 1.047 \, \text{弧度} \)
因此,正割值为 2 的角度约为 1.047 弧度或 60°。
例子 2:已知 \(\sec(\theta) = -2\),求对应的角度 \(\theta\):
解答:
\( \theta = \operatorname{arcsec}(-2) \approx 2.094 \, \text{弧度} \)
所以,正割值为 -2 的角度约为 2.094 弧度或 120°。
反正割函数的图形
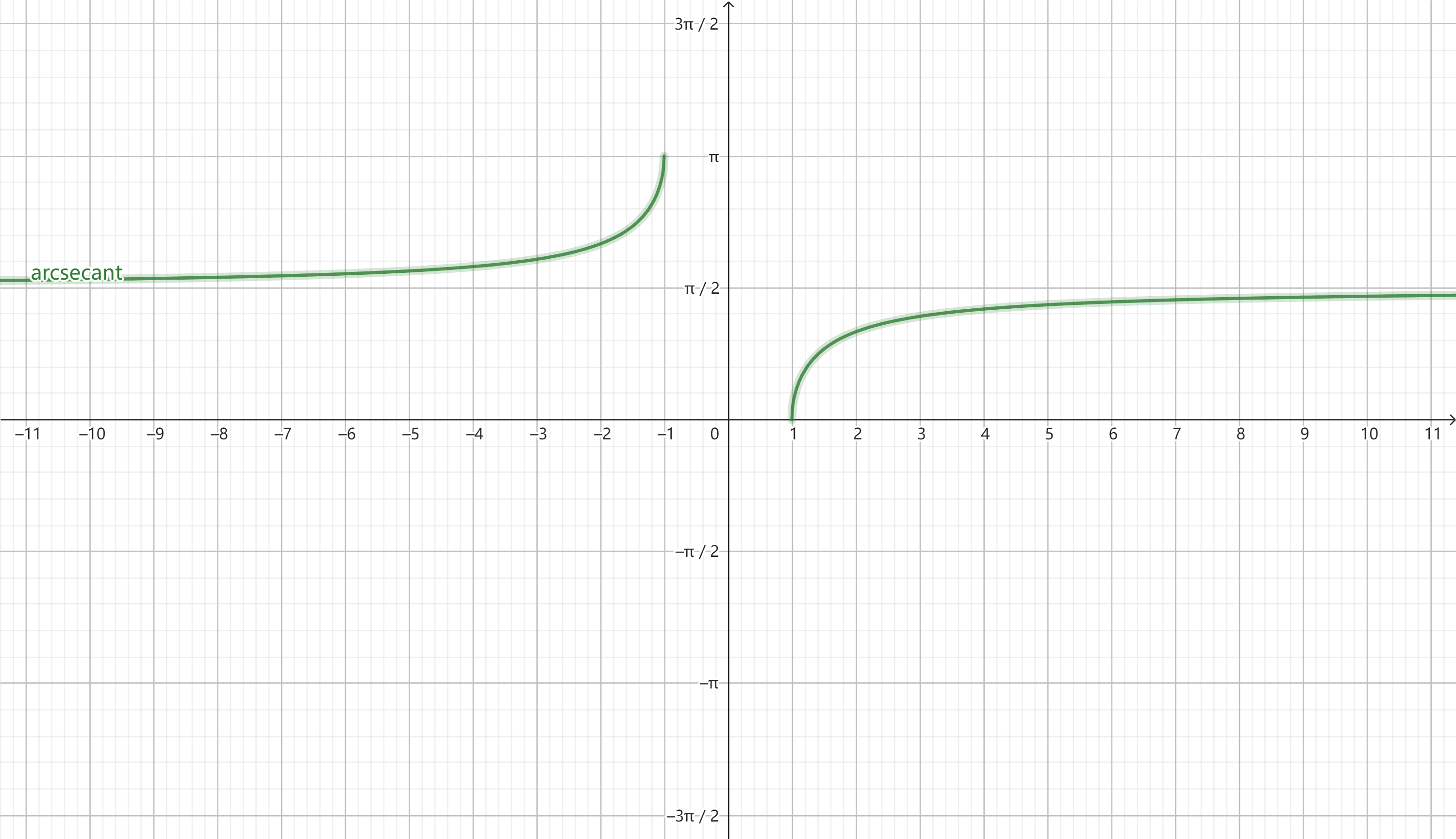
反正割函数的图形是两个单调递增的曲线段,范围从 \((-\infty, -1] \cup [1, +\infty)\),其值域为 \((0, \pi]\),不包含 \(\frac{\pi}{2}\)。图形的主要特性包括:
- 单调性:反正割在定义域内分为两部分,均为单调递增。
- 奇函数:反正割满足 \(\operatorname{arcsec}(-x) = \pi - \operatorname{arcsec}(x)\)。
反正割函数转换表格
| 正割值 | 角度 | 弧度 |
|---|---|---|
| 1 | 0° | 0 |
| 1.00015233 | 1° | \(\frac{\pi}{180}\) |
| 1.00060954 | 2° | \(\frac{\pi}{90}\) |
| 1.00137235 | 3° | \(\frac{\pi}{60}\) |
| 1.0024419 | 4° | \(\frac{\pi}{45}\) |
| 1.00381984 | 5° | \(\frac{\pi}{36}\) |
| 1.00550828 | 6° | \(\frac{\pi}{30}\) |
| 1.00750983 | 7° | \(\frac{7\pi}{180}\) |
| 1.00982757 | 8° | \(\frac{2\pi}{45}\) |
| 1.01246513 | 9° | \(\frac{\pi}{20}\) |
| 1.01542661 | 10° | \(\frac{\pi}{18}\) |
| 1.01871669 | 11° | \(\frac{11\pi}{180}\) |
| 1.02234059 | 12° | \(\frac{\pi}{15}\) |
| 1.02630411 | 13° | \(\frac{13\pi}{180}\) |
| 1.03061363 | 14° | \(\frac{7\pi}{90}\) |
| 1.03527618 | 15° | \(\frac{\pi}{12}\) |
| 1.04029944 | 16° | \(\frac{4\pi}{45}\) |
| 1.04569176 | 17° | \(\frac{17\pi}{180}\) |
| 1.05146222 | 18° | \(\frac{\pi}{10}\) |
| 1.05762068 | 19° | \(\frac{19\pi}{180}\) |
| 1.06417777 | 20° | \(\frac{\pi}{9}\) |
| 1.07114499 | 21° | \(\frac{7\pi}{60}\) |
| 1.07853474 | 22° | \(\frac{11\pi}{90}\) |
| 1.08636038 | 23° | \(\frac{23\pi}{180}\) |
| 1.09463628 | 24° | \(\frac{2\pi}{15}\) |
| 1.10337792 | 25° | \(\frac{5\pi}{36}\) |
| 1.11260194 | 26° | \(\frac{13\pi}{90}\) |
| 1.12232624 | 27° | \(\frac{3\pi}{20}\) |
| 1.13257005 | 28° | \(\frac{7\pi}{45}\) |
| 1.14335407 | 29° | \(\frac{29\pi}{180}\) |
| 1.15470054 | 30° | \(\frac{\pi}{6}\) |
| 1.1666334 | 31° | \(\frac{31\pi}{180}\) |
| 1.1791784 | 32° | \(\frac{8\pi}{45}\) |
| 1.19236329 | 33° | \(\frac{11\pi}{60}\) |
| 1.20621795 | 34° | \(\frac{17\pi}{90}\) |
| 1.22077459 | 35° | \(\frac{7\pi}{36}\) |
| 1.23606798 | 36° | \(\frac{\pi}{5}\) |
| 1.25213566 | 37° | \(\frac{37\pi}{180}\) |
| 1.26901822 | 38° | \(\frac{19\pi}{90}\) |
| 1.28675957 | 39° | \(\frac{13\pi}{60}\) |
| 1.30540729 | 40° | \(\frac{2\pi}{9}\) |
| 1.32501299 | 41° | \(\frac{41\pi}{180}\) |
| 1.34563273 | 42° | \(\frac{7\pi}{30}\) |
| 1.36732746 | 43° | \(\frac{43\pi}{180}\) |
| 1.39016359 | 44° | \(\frac{11\pi}{45}\) |
| 1.41421356 | 45° | \(\frac{\pi}{4}\) |
| 1.43955654 | 46° | \(\frac{23\pi}{90}\) |
| 1.46627919 | 47° | \(\frac{47\pi}{180}\) |
| 1.49447655 | 48° | \(\frac{4\pi}{15}\) |
| 1.52425309 | 49° | \(\frac{49\pi}{180}\) |
| 1.55572383 | 50° | \(\frac{5\pi}{18}\) |
| 1.58901573 | 51° | \(\frac{17\pi}{60}\) |
| 1.62426925 | 52° | \(\frac{13\pi}{45}\) |
| 1.66164014 | 53° | \(\frac{53\pi}{180}\) |
| 1.70130162 | 54° | \(\frac{3\pi}{10}\) |
| 1.7434468 | 55° | \(\frac{11\pi}{36}\) |
| 1.78829165 | 56° | \(\frac{14\pi}{45}\) |
| 1.83607846 | 57° | \(\frac{19\pi}{60}\) |
| 1.88707991 | 58° | \(\frac{29\pi}{90}\) |
| 1.94160403 | 59° | \(\frac{59\pi}{180}\) |
| 2 | 60° | \(\frac{\pi}{3}\) |
| 2.06266534 | 61° | \(\frac{61\pi}{180}\) |
| 2.13005447 | 62° | \(\frac{31\pi}{90}\) |
| 2.20268926 | 63° | \(\frac{7\pi}{20}\) |
| 2.28117203 | 64° | \(\frac{16\pi}{45}\) |
| 2.36620158 | 65° | \(\frac{13\pi}{36}\) |
| 2.45859334 | 66° | \(\frac{11\pi}{30}\) |
| 2.55930467 | 67° | \(\frac{67\pi}{180}\) |
| 2.66946716 | 68° | \(\frac{17\pi}{45}\) |
| 2.79042811 | 69° | \(\frac{23\pi}{60}\) |
| 2.9238044 | 70° | \(\frac{7\pi}{18}\) |
| 3.07155349 | 71° | \(\frac{71\pi}{180}\) |
| 3.23606798 | 72° | \(\frac{2\pi}{5}\) |
| 3.42030362 | 73° | \(\frac{73\pi}{180}\) |
| 3.62795528 | 74° | \(\frac{37\pi}{90}\) |
| 3.86370331 | 75° | \(\frac{5\pi}{12}\) |
| 4.13356549 | 76° | \(\frac{19\pi}{45}\) |
| 4.44541148 | 77° | \(\frac{77\pi}{180}\) |
| 4.80973434 | 78° | \(\frac{13\pi}{30}\) |
| 5.24084306 | 79° | \(\frac{79\pi}{180}\) |
| 5.75877048 | 80° | \(\frac{4\pi}{9}\) |
| 6.39245322 | 81° | \(\frac{9\pi}{20}\) |
| 7.18529653 | 82° | \(\frac{41\pi}{90}\) |
| 8.20550905 | 83° | \(\frac{83\pi}{180}\) |
| 9.56677223 | 84° | \(\frac{7\pi}{15}\) |
| 11.47371325 | 85° | \(\frac{17\pi}{36}\) |
| 14.33558703 | 86° | \(\frac{43\pi}{90}\) |
| 19.10732261 | 87° | \(\frac{29\pi}{60}\) |
| 28.65370835 | 88° | \(\frac{22\pi}{45}\) |
| 57.2986885 | 89° | \(\frac{89\pi}{180}\) |
| -57.2986885 | 91° | \(\frac{91\pi}{180}\) |
| -28.65370835 | 92° | \(\frac{23\pi}{45}\) |
| -19.10732261 | 93° | \(\frac{31\pi}{60}\) |
| -14.33558703 | 94° | \(\frac{47\pi}{90}\) |
| -11.47371325 | 95° | \(\frac{19\pi}{36}\) |
| -9.56677223 | 96° | \(\frac{8\pi}{15}\) |
| -8.20550905 | 97° | \(\frac{97\pi}{180}\) |
| -7.18529653 | 98° | \(\frac{49\pi}{90}\) |
| -6.39245322 | 99° | \(\frac{11\pi}{20}\) |
| -5.75877048 | 100° | \(\frac{5\pi}{9}\) |
| -5.24084306 | 101° | \(\frac{101\pi}{180}\) |
| -4.80973434 | 102° | \(\frac{17\pi}{30}\) |
| -4.44541148 | 103° | \(\frac{103\pi}{180}\) |
| -4.13356549 | 104° | \(\frac{26\pi}{45}\) |
| -3.86370331 | 105° | \(\frac{7\pi}{12}\) |
| -3.62795528 | 106° | \(\frac{53\pi}{90}\) |
| -3.42030362 | 107° | \(\frac{107\pi}{180}\) |
| -3.23606798 | 108° | \(\frac{3\pi}{5}\) |
| -3.07155349 | 109° | \(\frac{109\pi}{180}\) |
| -2.9238044 | 110° | \(\frac{11\pi}{18}\) |
| -2.79042811 | 111° | \(\frac{37\pi}{60}\) |
| -2.66946716 | 112° | \(\frac{28\pi}{45}\) |
| -2.55930467 | 113° | \(\frac{113\pi}{180}\) |
| -2.45859334 | 114° | \(\frac{19\pi}{30}\) |
| -2.36620158 | 115° | \(\frac{23\pi}{36}\) |
| -2.28117203 | 116° | \(\frac{29\pi}{45}\) |
| -2.20268926 | 117° | \(\frac{13\pi}{20}\) |
| -2.13005447 | 118° | \(\frac{59\pi}{90}\) |
| -2.06266534 | 119° | \(\frac{119\pi}{180}\) |
| -2 | 120° | \(\frac{2\pi}{3}\) |
| -1.94160403 | 121° | \(\frac{121\pi}{180}\) |
| -1.88707991 | 122° | \(\frac{61\pi}{90}\) |
| -1.83607846 | 123° | \(\frac{41\pi}{60}\) |
| -1.78829165 | 124° | \(\frac{31\pi}{45}\) |
| -1.7434468 | 125° | \(\frac{25\pi}{36}\) |
| -1.70130162 | 126° | \(\frac{7\pi}{10}\) |
| -1.66164014 | 127° | \(\frac{127\pi}{180}\) |
| -1.62426925 | 128° | \(\frac{32\pi}{45}\) |
| -1.58901573 | 129° | \(\frac{43\pi}{60}\) |
| -1.55572383 | 130° | \(\frac{13\pi}{18}\) |
| -1.52425309 | 131° | \(\frac{131\pi}{180}\) |
| -1.49447655 | 132° | \(\frac{11\pi}{15}\) |
| -1.46627919 | 133° | \(\frac{133\pi}{180}\) |
| -1.43955654 | 134° | \(\frac{67\pi}{90}\) |
| -1.41421356 | 135° | \(\frac{3\pi}{4}\) |
| -1.39016359 | 136° | \(\frac{34\pi}{45}\) |
| -1.36732746 | 137° | \(\frac{137\pi}{180}\) |
| -1.34563273 | 138° | \(\frac{23\pi}{30}\) |
| -1.32501299 | 139° | \(\frac{139\pi}{180}\) |
| -1.30540729 | 140° | \(\frac{7\pi}{9}\) |
| -1.28675957 | 141° | \(\frac{47\pi}{60}\) |
| -1.26901822 | 142° | \(\frac{71\pi}{90}\) |
| -1.25213566 | 143° | \(\frac{143\pi}{180}\) |
| -1.23606798 | 144° | \(\frac{4\pi}{5}\) |
| -1.22077459 | 145° | \(\frac{29\pi}{36}\) |
| -1.20621795 | 146° | \(\frac{73\pi}{90}\) |
| -1.19236329 | 147° | \(\frac{49\pi}{60}\) |
| -1.1791784 | 148° | \(\frac{37\pi}{45}\) |
| -1.1666334 | 149° | \(\frac{149\pi}{180}\) |
| -1.15470054 | 150° | \(\frac{5\pi}{6}\) |
| -1.14335407 | 151° | \(\frac{151\pi}{180}\) |
| -1.13257005 | 152° | \(\frac{38\pi}{45}\) |
| -1.12232624 | 153° | \(\frac{17\pi}{20}\) |
| -1.11260194 | 154° | \(\frac{77\pi}{90}\) |
| -1.10337792 | 155° | \(\frac{31\pi}{36}\) |
| -1.09463628 | 156° | \(\frac{13\pi}{15}\) |
| -1.08636038 | 157° | \(\frac{157\pi}{180}\) |
| -1.07853474 | 158° | \(\frac{79\pi}{90}\) |
| -1.07114499 | 159° | \(\frac{53\pi}{60}\) |
| -1.06417777 | 160° | \(\frac{8\pi}{9}\) |
| -1.05762068 | 161° | \(\frac{161\pi}{180}\) |
| -1.05146222 | 162° | \(\frac{9\pi}{10}\) |
| -1.04569176 | 163° | \(\frac{163\pi}{180}\) |
| -1.04029944 | 164° | \(\frac{41\pi}{45}\) |
| -1.03527618 | 165° | \(\frac{11\pi}{12}\) |
| -1.03061363 | 166° | \(\frac{83\pi}{90}\) |
| -1.02630411 | 167° | \(\frac{167\pi}{180}\) |
| -1.02234059 | 168° | \(\frac{14\pi}{15}\) |
| -1.01871669 | 169° | \(\frac{169\pi}{180}\) |
| -1.01542661 | 170° | \(\frac{17\pi}{18}\) |
| -1.01246513 | 171° | \(\frac{19\pi}{20}\) |
| -1.00982757 | 172° | \(\frac{43\pi}{45}\) |
| -1.00750983 | 173° | \(\frac{173\pi}{180}\) |
| -1.00550828 | 174° | \(\frac{29\pi}{30}\) |
| -1.00381984 | 175° | \(\frac{35\pi}{36}\) |
| -1.0024419 | 176° | \(\frac{44\pi}{45}\) |
| -1.00137235 | 177° | \(\frac{59\pi}{60}\) |
| -1.00060954 | 178° | \(\frac{89\pi}{90}\) |
| -1.00015233 | 179° | \(\frac{179\pi}{180}\) |
| -1 | 180° | π |