反正切计算器
输入正切值,计算对应的角度和弧度。
反正切计算
角度
弧度
什么是反正切函数
反正切函数(Arctangent function)是正切函数的反函数,通常用符号 \(\arctan(x)\) 或 \(\tan^{-1}(x)\) 表示,用于计算给定正切值对应的角度。对于正切函数 \(y = \tan(\theta)\),反正切函数定义为: \( \theta = \arctan(x) \) 其中,\(-\infty < x < \infty\) 且 \(-\frac{\pi}{2} < \theta < \frac{\pi}{2}\)。反正切的值域为 \(\left(- \frac{\pi}{2}, \frac{\pi}{2}\right)\)。
示例
例子 1:假设已知 \(\tan(\theta) = 1\),求对应的角度 \(\theta\):
解答:
\( \theta = \arctan(1) = \frac{\pi}{4} \approx 0.7854 \, \text{弧度} \)
因此,正切值为 1 的角度是 \(\frac{\pi}{4}\) 或 45°。
例子 2:已知 \(\tan(\theta) = 0\),求对应的角度 \(\theta\):
解答:
\( \theta = \arctan(0) = 0 \)
所以,正切值为 0 的角度是 0 。
反正切函数图形
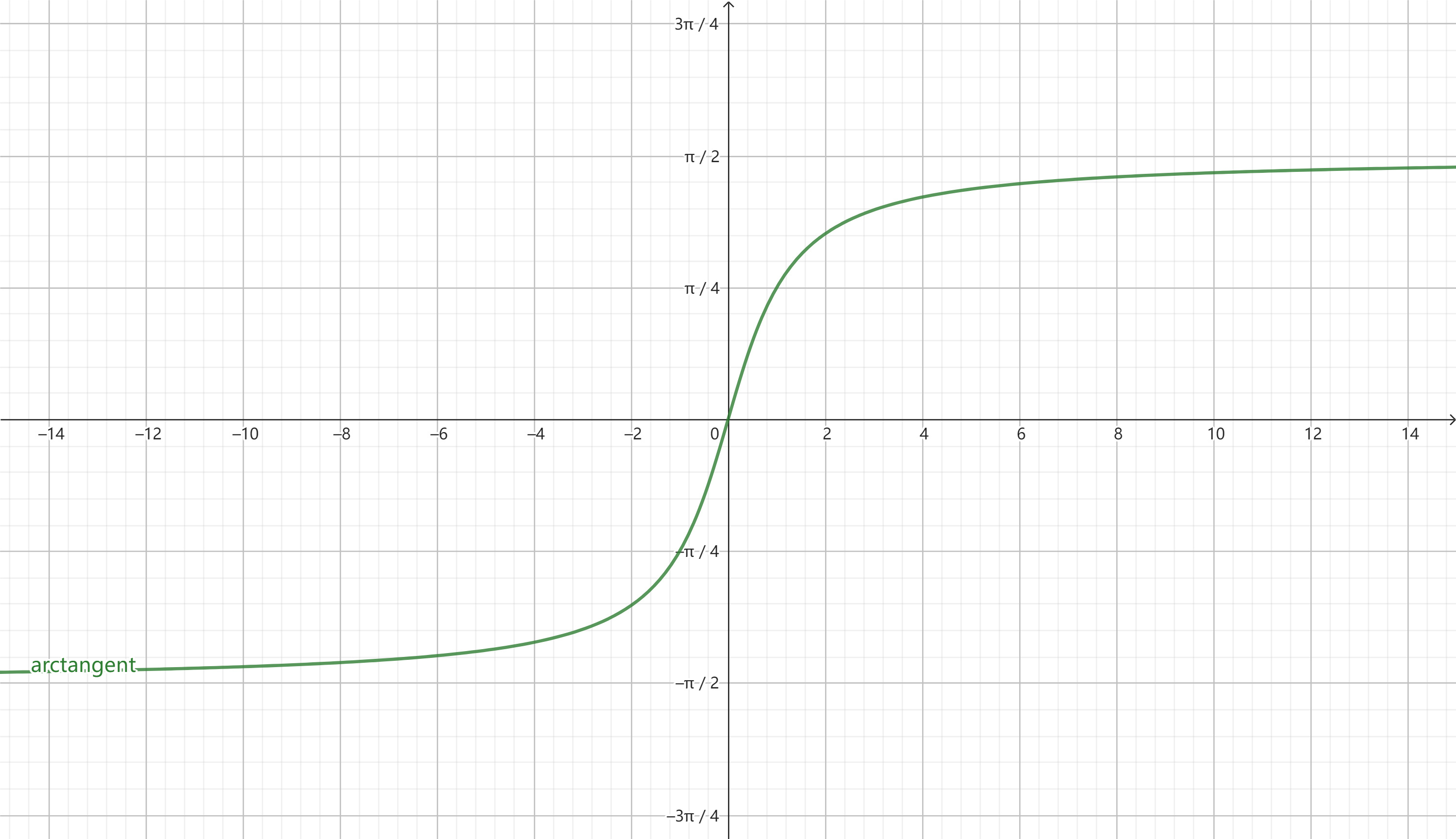
反正切函数的图形是一条单调递增的曲线,范围从 \(-\infty\) 到 \(+\infty\),其值域为 \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)。图形的主要特性包括:
- 单调性:在定义域内,反正切函数是单调递增的。
- 奇函数:反正切是奇函数,满足 \(\arctan(-x) = -\arctan(x)\),即关于原点对称。
反正切函数转换表格
| 正切值 | 角度 | 弧度 |
|---|---|---|
| -57.28996163 | -89° | \(\frac{-89\pi}{180}\) |
| -28.63625328 | -88° | \(\frac{-22\pi}{45}\) |
| -19.08113669 | -87° | \(\frac{-29\pi}{60}\) |
| -14.30066626 | -86° | \(\frac{-43\pi}{90}\) |
| -11.4300523 | -85° | \(\frac{-17\pi}{36}\) |
| -9.51436445 | -84° | \(\frac{-7\pi}{15}\) |
| -8.14434643 | -83° | \(\frac{-83\pi}{180}\) |
| -7.11536972 | -82° | \(\frac{-41\pi}{90}\) |
| -6.31375151 | -81° | \(\frac{-9\pi}{20}\) |
| -5.67128182 | -80° | \(\frac{-4\pi}{9}\) |
| -5.14455402 | -79° | \(\frac{-79\pi}{180}\) |
| -4.70463011 | -78° | \(\frac{-13\pi}{30}\) |
| -4.33147587 | -77° | \(\frac{-77\pi}{180}\) |
| -4.01078093 | -76° | \(\frac{-19\pi}{45}\) |
| -3.73205081 | -75° | \(\frac{-5\pi}{12}\) |
| -3.48741444 | -74° | \(\frac{-37\pi}{90}\) |
| -3.27085262 | -73° | \(\frac{-73\pi}{180}\) |
| -3.07768354 | -72° | \(\frac{-2\pi}{5}\) |
| -2.90421088 | -71° | \(\frac{-71\pi}{180}\) |
| -2.74747742 | -70° | \(\frac{-7\pi}{18}\) |
| -2.60508906 | -69° | \(\frac{-23\pi}{60}\) |
| -2.47508685 | -68° | \(\frac{-17\pi}{45}\) |
| -2.35585237 | -67° | \(\frac{-67\pi}{180}\) |
| -2.24603677 | -66° | \(\frac{-11\pi}{30}\) |
| -2.14450692 | -65° | \(\frac{-13\pi}{36}\) |
| -2.05030384 | -64° | \(\frac{-16\pi}{45}\) |
| -1.96261051 | -63° | \(\frac{-7\pi}{20}\) |
| -1.88072647 | -62° | \(\frac{-31\pi}{90}\) |
| -1.80404776 | -61° | \(\frac{-61\pi}{180}\) |
| -1.73205081 | -60° | \(\frac{-\pi}{3}\) |
| -1.66427948 | -59° | \(\frac{-59\pi}{180}\) |
| -1.60033453 | -58° | \(\frac{-29\pi}{90}\) |
| -1.53986496 | -57° | \(\frac{-19\pi}{60}\) |
| -1.48256097 | -56° | \(\frac{-14\pi}{45}\) |
| -1.42814801 | -55° | \(\frac{-11\pi}{36}\) |
| -1.37638192 | -54° | \(\frac{-3\pi}{10}\) |
| -1.32704482 | -53° | \(\frac{-53\pi}{180}\) |
| -1.27994163 | -52° | \(\frac{-13\pi}{45}\) |
| -1.23489716 | -51° | \(\frac{-17\pi}{60}\) |
| -1.19175359 | -50° | \(\frac{-5\pi}{18}\) |
| -1.15036841 | -49° | \(\frac{-49\pi}{180}\) |
| -1.11061251 | -48° | \(\frac{-4\pi}{15}\) |
| -1.07236871 | -47° | \(\frac{-47\pi}{180}\) |
| -1.03553031 | -46° | \(\frac{-23\pi}{90}\) |
| -1 | -45° | \(\frac{-\pi}{4}\) |
| -0.96568877 | -44° | \(\frac{-11\pi}{45}\) |
| -0.93251509 | -43° | \(\frac{-43\pi}{180}\) |
| -0.90040404 | -42° | \(\frac{-7\pi}{30}\) |
| -0.86928674 | -41° | \(\frac{-41\pi}{180}\) |
| -0.83909963 | -40° | \(\frac{-2\pi}{9}\) |
| -0.80978403 | -39° | \(\frac{-13\pi}{60}\) |
| -0.78128563 | -38° | \(\frac{-19\pi}{90}\) |
| -0.75355405 | -37° | \(\frac{-37\pi}{180}\) |
| -0.72654253 | -36° | \(\frac{-\pi}{5}\) |
| -0.70020754 | -35° | \(\frac{-7\pi}{36}\) |
| -0.67450852 | -34° | \(\frac{-17\pi}{90}\) |
| -0.64940759 | -33° | \(\frac{-11\pi}{60}\) |
| -0.62486935 | -32° | \(\frac{-8\pi}{45}\) |
| -0.60086062 | -31° | \(\frac{-31\pi}{180}\) |
| -0.57735027 | -30° | \(\frac{-\pi}{6}\) |
| -0.55430905 | -29° | \(\frac{-29\pi}{180}\) |
| -0.53170943 | -28° | \(\frac{-7\pi}{45}\) |
| -0.50952545 | -27° | \(\frac{-3\pi}{20}\) |
| -0.48773259 | -26° | \(\frac{-13\pi}{90}\) |
| -0.46630766 | -25° | \(\frac{-5\pi}{36}\) |
| -0.44522869 | -24° | \(\frac{-2\pi}{15}\) |
| -0.42447482 | -23° | \(\frac{-23\pi}{180}\) |
| -0.40402623 | -22° | \(\frac{-11\pi}{90}\) |
| -0.38386404 | -21° | \(\frac{-7\pi}{60}\) |
| -0.36397023 | -20° | \(\frac{-\pi}{9}\) |
| -0.34432761 | -19° | \(\frac{-19\pi}{180}\) |
| -0.3249197 | -18° | \(\frac{-\pi}{10}\) |
| -0.30573068 | -17° | \(\frac{-17\pi}{180}\) |
| -0.28674539 | -16° | \(\frac{-4\pi}{45}\) |
| -0.26794919 | -15° | \(\frac{-\pi}{12}\) |
| -0.249328 | -14° | \(\frac{-7\pi}{90}\) |
| -0.23086819 | -13° | \(\frac{-13\pi}{180}\) |
| -0.21255656 | -12° | \(\frac{-\pi}{15}\) |
| -0.19438031 | -11° | \(\frac{-11\pi}{180}\) |
| -0.17632698 | -10° | \(\frac{-\pi}{18}\) |
| -0.15838444 | -9° | \(\frac{-\pi}{20}\) |
| -0.14054083 | -8° | \(\frac{-2\pi}{45}\) |
| -0.12278456 | -7° | \(\frac{-7\pi}{180}\) |
| -0.10510424 | -6° | \(\frac{-\pi}{30}\) |
| -0.08748866 | -5° | \(\frac{-\pi}{36}\) |
| -0.06992681 | -4° | \(\frac{-\pi}{45}\) |
| -0.05240778 | -3° | \(\frac{-\pi}{60}\) |
| -0.03492077 | -2° | \(\frac{-\pi}{90}\) |
| -0.01745506 | -1° | \(\frac{-\pi}{180}\) |
| 0 | 0° | 0 |
| 0.01745506 | 1° | \(\frac{\pi}{180}\) |
| 0.03492077 | 2° | \(\frac{\pi}{90}\) |
| 0.05240778 | 3° | \(\frac{\pi}{60}\) |
| 0.06992681 | 4° | \(\frac{\pi}{45}\) |
| 0.08748866 | 5° | \(\frac{\pi}{36}\) |
| 0.10510424 | 6° | \(\frac{\pi}{30}\) |
| 0.12278456 | 7° | \(\frac{7\pi}{180}\) |
| 0.14054083 | 8° | \(\frac{2\pi}{45}\) |
| 0.15838444 | 9° | \(\frac{\pi}{20}\) |
| 0.17632698 | 10° | \(\frac{\pi}{18}\) |
| 0.19438031 | 11° | \(\frac{11\pi}{180}\) |
| 0.21255656 | 12° | \(\frac{\pi}{15}\) |
| 0.23086819 | 13° | \(\frac{13\pi}{180}\) |
| 0.249328 | 14° | \(\frac{7\pi}{90}\) |
| 0.26794919 | 15° | \(\frac{\pi}{12}\) |
| 0.28674539 | 16° | \(\frac{4\pi}{45}\) |
| 0.30573068 | 17° | \(\frac{17\pi}{180}\) |
| 0.3249197 | 18° | \(\frac{\pi}{10}\) |
| 0.34432761 | 19° | \(\frac{19\pi}{180}\) |
| 0.36397023 | 20° | \(\frac{\pi}{9}\) |
| 0.38386404 | 21° | \(\frac{7\pi}{60}\) |
| 0.40402623 | 22° | \(\frac{11\pi}{90}\) |
| 0.42447482 | 23° | \(\frac{23\pi}{180}\) |
| 0.44522869 | 24° | \(\frac{2\pi}{15}\) |
| 0.46630766 | 25° | \(\frac{5\pi}{36}\) |
| 0.48773259 | 26° | \(\frac{13\pi}{90}\) |
| 0.50952545 | 27° | \(\frac{3\pi}{20}\) |
| 0.53170943 | 28° | \(\frac{7\pi}{45}\) |
| 0.55430905 | 29° | \(\frac{29\pi}{180}\) |
| 0.57735027 | 30° | \(\frac{\pi}{6}\) |
| 0.60086062 | 31° | \(\frac{31\pi}{180}\) |
| 0.62486935 | 32° | \(\frac{8\pi}{45}\) |
| 0.64940759 | 33° | \(\frac{11\pi}{60}\) |
| 0.67450852 | 34° | \(\frac{17\pi}{90}\) |
| 0.70020754 | 35° | \(\frac{7\pi}{36}\) |
| 0.72654253 | 36° | \(\frac{\pi}{5}\) |
| 0.75355405 | 37° | \(\frac{37\pi}{180}\) |
| 0.78128563 | 38° | \(\frac{19\pi}{90}\) |
| 0.80978403 | 39° | \(\frac{13\pi}{60}\) |
| 0.83909963 | 40° | \(\frac{2\pi}{9}\) |
| 0.86928674 | 41° | \(\frac{41\pi}{180}\) |
| 0.90040404 | 42° | \(\frac{7\pi}{30}\) |
| 0.93251509 | 43° | \(\frac{43\pi}{180}\) |
| 0.96568877 | 44° | \(\frac{11\pi}{45}\) |
| 1 | 45° | \(\frac{\pi}{4}\) |
| 1.03553031 | 46° | \(\frac{23\pi}{90}\) |
| 1.07236871 | 47° | \(\frac{47\pi}{180}\) |
| 1.11061251 | 48° | \(\frac{4\pi}{15}\) |
| 1.15036841 | 49° | \(\frac{49\pi}{180}\) |
| 1.19175359 | 50° | \(\frac{5\pi}{18}\) |
| 1.23489716 | 51° | \(\frac{17\pi}{60}\) |
| 1.27994163 | 52° | \(\frac{13\pi}{45}\) |
| 1.32704482 | 53° | \(\frac{53\pi}{180}\) |
| 1.37638192 | 54° | \(\frac{3\pi}{10}\) |
| 1.42814801 | 55° | \(\frac{11\pi}{36}\) |
| 1.48256097 | 56° | \(\frac{14\pi}{45}\) |
| 1.53986496 | 57° | \(\frac{19\pi}{60}\) |
| 1.60033453 | 58° | \(\frac{29\pi}{90}\) |
| 1.66427948 | 59° | \(\frac{59\pi}{180}\) |
| 1.73205081 | 60° | \(\frac{\pi}{3}\) |
| 1.80404776 | 61° | \(\frac{61\pi}{180}\) |
| 1.88072647 | 62° | \(\frac{31\pi}{90}\) |
| 1.96261051 | 63° | \(\frac{7\pi}{20}\) |
| 2.05030384 | 64° | \(\frac{16\pi}{45}\) |
| 2.14450692 | 65° | \(\frac{13\pi}{36}\) |
| 2.24603677 | 66° | \(\frac{11\pi}{30}\) |
| 2.35585237 | 67° | \(\frac{67\pi}{180}\) |
| 2.47508685 | 68° | \(\frac{17\pi}{45}\) |
| 2.60508906 | 69° | \(\frac{23\pi}{60}\) |
| 2.74747742 | 70° | \(\frac{7\pi}{18}\) |
| 2.90421088 | 71° | \(\frac{71\pi}{180}\) |
| 3.07768354 | 72° | \(\frac{2\pi}{5}\) |
| 3.27085262 | 73° | \(\frac{73\pi}{180}\) |
| 3.48741444 | 74° | \(\frac{37\pi}{90}\) |
| 3.73205081 | 75° | \(\frac{5\pi}{12}\) |
| 4.01078093 | 76° | \(\frac{19\pi}{45}\) |
| 4.33147587 | 77° | \(\frac{77\pi}{180}\) |
| 4.70463011 | 78° | \(\frac{13\pi}{30}\) |
| 5.14455402 | 79° | \(\frac{79\pi}{180}\) |
| 5.67128182 | 80° | \(\frac{4\pi}{9}\) |
| 6.31375151 | 81° | \(\frac{9\pi}{20}\) |
| 7.11536972 | 82° | \(\frac{41\pi}{90}\) |
| 8.14434643 | 83° | \(\frac{83\pi}{180}\) |
| 9.51436445 | 84° | \(\frac{7\pi}{15}\) |
| 11.4300523 | 85° | \(\frac{17\pi}{36}\) |
| 14.30066626 | 86° | \(\frac{43\pi}{90}\) |
| 19.08113669 | 87° | \(\frac{29\pi}{60}\) |
| 28.63625328 | 88° | \(\frac{22\pi}{45}\) |
| 57.28996163 | 89° | \(\frac{89\pi}{180}\) |