弓形计算器
输入弓形的圆心角(度数或弧度)和一个已知属性值(如半径、弦长、弧长、面积等),快速计算弓形的其它几何属性。
计算弓形的半径、弦长、弧长、周长、面积、高度等
半径
弦长
弧长
高度
周长
面积
什么是弓形?
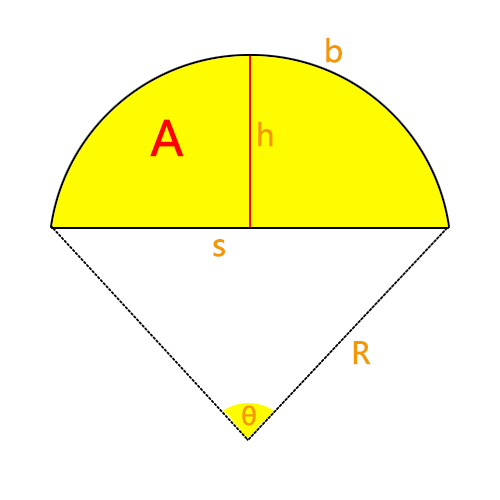
弓形是由圆的弧和该弧所对应的弦所围成的区域,它是由一个圆心角(度数或弧度)以及弧长、弦长、高度、周长或面积等属性描述的几何形状。
如何计算弓形的属性?
假设弓形对应的圆心角为 θ(以弧度为单位),半径是 r。
弦长
弦长是连接圆上两个点的直线距离,公式为: \( \text{Chord Length} = 2 \times r \times \sin\left(\frac{\theta}{2}\right) \)
弧长
弧长是圆弧的长度,可以通过以下公式计算: \( \text{Arc Length} = \theta \times r \)
高度
高度是弓形的顶点到弦的垂直距离,公式是: \( h = r - \sqrt{r^2 - \left(\frac{\text{Chord Length}}{2}\right)^2} \) 其中,Chord Length 是弦长。
周长
弓形的周长是弧长与弦长之和: \( P = \text{Arc Length} + \text{Chord Length} \)
面积
弓形的面积是由圆心角对应的扇形面积减去三角形面积: \( A = \frac{1}{2} r^2 (\theta - \sin\theta) \)
示例:已知圆心角 θ = 60°,半径 r = 10,计算弓形的弦长、弧长、高度、周长和面积。
解答:
角度转为弧度:
\( \theta = 60^\circ = \frac{60 \times \pi}{180} = \frac{\pi}{3} \text{ rad} \)
弦长:
\( \text{Chord Length} = 2 \times 10 \times \sin\left(\frac{\pi}{6}\right) = 20 \times \frac{1}{2} = 10 \)
弧长:
\( \text{Arc Length} = \theta \times r = \frac{\pi}{3} \times 10 \approx 10.47 \)
高度:
\( h = 10 - \sqrt{10^2 - \left(\frac{10}{2}\right)^2} = 10 - \sqrt{100 - 25} \approx 1.34 \)
周长:
\( P = \text{Arc Length} + \text{Chord Length} = 10.47 + 10 = 20.47 \)
面积:
\( A = \frac{1}{2} \times 10^2 \times \left(\frac{\pi}{3} - \sin\left(\frac{\pi}{3}\right)\right) \approx 9.06 \)