椭圆计算器
输入半长轴和半短轴,快速计算椭圆的周长、面积和离心率。
计算椭圆的周长、面积和离心率
周长
面积
离心率
什么是椭圆?
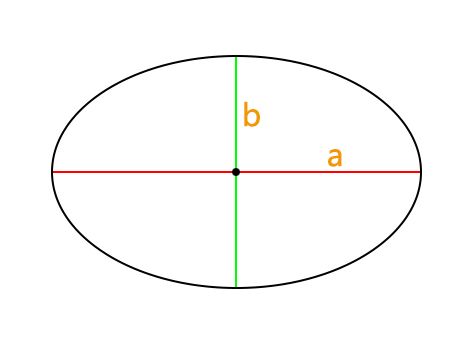
椭圆是平面上与一个焦点及两条定焦线的距离之和保持恒定的点的轨迹。椭圆的两条轴分别是半长轴和半短轴。半长轴是椭圆沿最长方向的半径,而半短轴是椭圆沿最短方向的半径。椭圆的周长、面积和离心率等可以通过已知的半长轴和半短轴来计算。
如何计算椭圆周长?
由于椭圆周长的精确计算公式是非常复杂的,通常使用近似公式: \( P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \) 其中 a 为半长轴,b 为半短轴。
如何计算椭圆面积?
椭圆的面积计算公式为: \( A = \pi a b \) 其中 a 为半长轴,b 为半短轴。
如何计算椭圆离心率?
离心率 e 表示椭圆的扁平程度,计算公式为: \( e = \sqrt{1 - \frac{b^2}{a^2}} \) 其中 a 为半长轴,b 为半短轴。
示例
例子 1:已知椭圆的半长轴为 6,半短轴为 4,计算椭圆的周长、面积和离心率。
解答:
计算周长:
\( P \approx \pi \left[ 3(6 + 4) - \sqrt{(3 \times 6 + 4)(6 + 3 \times 4)} \right] \approx 31.73 \)
计算面积:
\( A = \pi \times 6 \times 4 = 24\pi \approx 75.398 \)
计算离心率:
\( e = \sqrt{1 - \frac{4^2}{6^2}} \approx 0.745 \)
例子 2:已知椭圆的半长轴为 10,半短轴为 6,计算椭圆的周长、面积和离心率。
解答:
计算周长:
\( P \approx \pi \left[ 3(10 + 6) - \sqrt{(3 \times 10 + 6)(10 + 3 \times 6)} \right] \approx 51.054 \)
计算面积:
\( A = \pi \times 10 \times 6 = 60\pi \approx 188.496 \)
计算离心率:
\( e = \sqrt{1 - \frac{6^2}{10^2}} = \sqrt{0.64} = 0.8 \)