三角形数计算器

输入一个数字，快速判断其是否为三角形数，或输入起止范围生成范围内所有三角形数。

什么是三角形数？

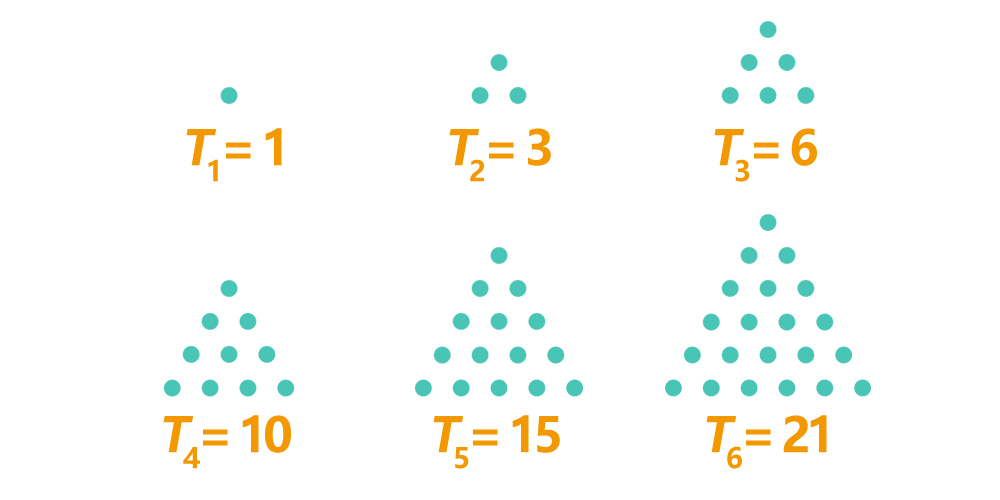
三角形数是指可以用等边三角形的点数排列成的数字。第 \(n\) 个三角形数可以通过公式 \(T_n = \frac{n(n + 1)}{2}\) 计算得到，其中 \(n\) 是正整数。

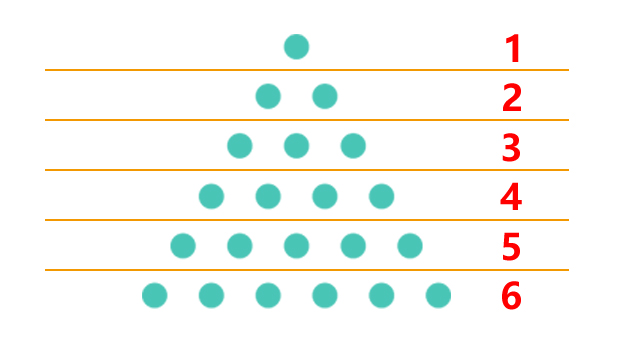
一个数 \(x\) 是三角形数当且仅当存在一个正整数 \(n\)，使得 \(x = \frac{n(n + 1)}{2} \)。即每一行的点数刚好构成一个等差序列，起始项为1，公差为1，总点数（正整数 \(x\) ）可以用等差序列求和公式算出。

解答：

\(n = \frac{-1 + \sqrt{1 + 8 \cdot 10}}{2} = \frac{-1 + \sqrt{81}}{2} = 4\)

所以，10 是三角形数。

解答：

\(n = \frac{-1 + \sqrt{1 + 8 \cdot 36}}{2} = \frac{-1 + \sqrt{289}}{2} = \frac{16}{2} = 8\)

因此，36 是三角形数。

解答：

\(n = \frac{-1 + \sqrt{1 + 8 \cdot 150}}{2} = \frac{-1 + \sqrt{1201}}{2} \approx \frac{34.64}{2} \approx 17.32\)

所以，150 不是三角形数。