正矢计算器
输入角度或弧度,快速计算对应的正矢值。
正矢计算
结果
什么是正矢函数
正矢函数(Versine function),通常用 \(\text{versin}(\theta)\) 表示,是一种历史悠久的三角函数。在直角三角形中,正矢函数的公式为: \( \text{versin}(\theta) = 1 - \cos(\theta) \) 这表明正矢函数是余弦函数的补量,适合描述余弦偏差或距离的变化。
例如,\(\theta = 60^\circ\) 时: \( \text{versin}(60^\circ) = 1 - \cos(60^\circ) = 1 - 0.5 = 0.5 \)
正矢函数图形
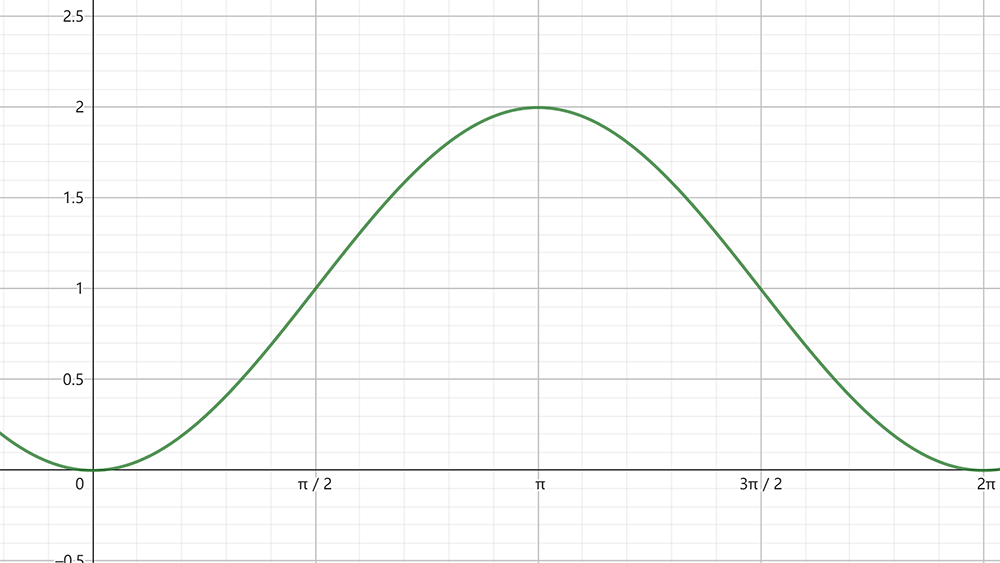
正矢函数的图形是正弦波的正向偏移,具有以下特性:
- 周期性:正矢函数的周期为 \(2\pi\)。
- 定义域:正矢函数的定义域为所有实数 \(\mathbb{R}\)。
- 值域:\(\text{versin}(\theta) \in [0, 2]\)。
- 振幅:最大值为 2,最小值为 0。
- 波形特性:正矢函数随 \(\theta\) 增加而波动,在 \(0\) 和 \(2\pi\) 处达到最小值(0),在 \(\pi\) 处达到最大值(2)。
正矢函数转换表
| 角度 | 弧度 | 正矢值 |
|---|---|---|
| 0° | 0 | 0 |
| 5° | \(\frac{\pi}{36}\) | 0.0038053 |
| 10° | \(\frac{\pi}{18}\) | 0.01519225 |
| 15° | \(\frac{\pi}{12}\) | 0.03407417 |
| 20° | \(\frac{\pi}{9}\) | 0.06030738 |
| 25° | \(\frac{5\pi}{36}\) | 0.09369221 |
| 30° | \(\frac{\pi}{6}\) | 0.1339746 |
| 35° | \(\frac{7\pi}{36}\) | 0.18084796 |
| 40° | \(\frac{2\pi}{9}\) | 0.23395556 |
| 45° | \(\frac{\pi}{4}\) | 0.29289322 |
| 50° | \(\frac{5\pi}{18}\) | 0.35721239 |
| 55° | \(\frac{11\pi}{36}\) | 0.42642356 |
| 60° | \(\frac{\pi}{3}\) | 0.5 |
| 65° | \(\frac{13\pi}{36}\) | 0.57738174 |
| 70° | \(\frac{7\pi}{18}\) | 0.65797986 |
| 75° | \(\frac{5\pi}{12}\) | 0.74118095 |
| 80° | \(\frac{4\pi}{9}\) | 0.82635182 |
| 85° | \(\frac{17\pi}{36}\) | 0.91284426 |
| 90° | \(\frac{\pi}{2}\) | 1 |
| 95° | \(\frac{19\pi}{36}\) | 1.08715574 |
| 100° | \(\frac{5\pi}{9}\) | 1.17364818 |
| 105° | \(\frac{7\pi}{12}\) | 1.25881905 |
| 110° | \(\frac{11\pi}{18}\) | 1.34202014 |
| 115° | \(\frac{23\pi}{36}\) | 1.42261826 |
| 120° | \(\frac{2\pi}{3}\) | 1.5 |
| 125° | \(\frac{25\pi}{36}\) | 1.57357644 |
| 130° | \(\frac{13\pi}{18}\) | 1.64278761 |
| 135° | \(\frac{3\pi}{4}\) | 1.70710678 |
| 140° | \(\frac{7\pi}{9}\) | 1.76604444 |
| 145° | \(\frac{29\pi}{36}\) | 1.81915204 |
| 150° | \(\frac{5\pi}{6}\) | 1.8660254 |
| 155° | \(\frac{31\pi}{36}\) | 1.90630779 |
| 160° | \(\frac{8\pi}{9}\) | 1.93969262 |
| 165° | \(\frac{11\pi}{12}\) | 1.96592583 |
| 170° | \(\frac{17\pi}{18}\) | 1.98480775 |
| 175° | \(\frac{35\pi}{36}\) | 1.9961947 |
| 180° | π | 2 |
| 185° | \(\frac{37\pi}{36}\) | 1.9961947 |
| 190° | \(\frac{19\pi}{18}\) | 1.98480775 |
| 195° | \(\frac{13\pi}{12}\) | 1.96592583 |
| 200° | \(\frac{10\pi}{9}\) | 1.93969262 |
| 205° | \(\frac{41\pi}{36}\) | 1.90630779 |
| 210° | \(\frac{7\pi}{6}\) | 1.8660254 |
| 215° | \(\frac{43\pi}{36}\) | 1.81915204 |
| 220° | \(\frac{11\pi}{9}\) | 1.76604444 |
| 225° | \(\frac{5\pi}{4}\) | 1.70710678 |
| 230° | \(\frac{23\pi}{18}\) | 1.64278761 |
| 235° | \(\frac{47\pi}{36}\) | 1.57357644 |
| 240° | \(\frac{4\pi}{3}\) | 1.5 |
| 245° | \(\frac{49\pi}{36}\) | 1.42261826 |
| 250° | \(\frac{25\pi}{18}\) | 1.34202014 |
| 255° | \(\frac{17\pi}{12}\) | 1.25881905 |
| 260° | \(\frac{13\pi}{9}\) | 1.17364818 |
| 265° | \(\frac{53\pi}{36}\) | 1.08715574 |
| 270° | \(\frac{3\pi}{2}\) | 1 |
| 275° | \(\frac{55\pi}{36}\) | 0.91284426 |
| 280° | \(\frac{14\pi}{9}\) | 0.82635182 |
| 285° | \(\frac{19\pi}{12}\) | 0.74118095 |
| 290° | \(\frac{29\pi}{18}\) | 0.65797986 |
| 295° | \(\frac{59\pi}{36}\) | 0.57738174 |
| 300° | \(\frac{5\pi}{3}\) | 0.5 |
| 305° | \(\frac{61\pi}{36}\) | 0.42642356 |
| 310° | \(\frac{31\pi}{18}\) | 0.35721239 |
| 315° | \(\frac{7\pi}{4}\) | 0.29289322 |
| 320° | \(\frac{16\pi}{9}\) | 0.23395556 |
| 325° | \(\frac{65\pi}{36}\) | 0.18084796 |
| 330° | \(\frac{11\pi}{6}\) | 0.1339746 |
| 335° | \(\frac{67\pi}{36}\) | 0.09369221 |
| 340° | \(\frac{17\pi}{9}\) | 0.06030738 |
| 345° | \(\frac{23\pi}{12}\) | 0.03407417 |
| 350° | \(\frac{35\pi}{18}\) | 0.01519225 |
| 355° | \(\frac{71\pi}{36}\) | 0.0038053 |
| 360° | 2π | 0 |